Логистическая регрессия и дары машинного обучения
Математическая истина, независимо от того, в Париже или в Тулузе, одна и та же.
Блез Паскаль
Логистическая регрессия – алгоритм с секретом. Нам понадобится небольшое предисловие о задачах машинного обучения в целом, чтобы понять, для какой цели применяется этот алгоритм. Это же регрессия, верно? Давайте разбираться.
Какие задачи решает машинное обучение:
- Регрессия осуществляет прогноз. На входе – признаки (features) объектов выборки, на выходе – вещественное число (стоимость товара, ожидаемая прибыль и т. д.).
- Классификация, удивительное дело, осуществляет классификацию по категориям. На входе – набор признаков. На выходе – «да» или «нет», иногда еще «не знаю/нейтральный класс». Если вы пушистый, любите колбасу, не работаете и большую часть времени спите, возможно, вы – кот. Как видите, всё зависит от адекватности набора признаков на входе.
- Кластеризация. Здесь на входе может быть неразмеченный набор данных, так как это обучение без учителя. На выходе – различные группы: потребительские сегменты и группы конкурентов в бизнесе, тематическое моделирование в обработке естественного языка, группы симптомов в биоинформатике и медицине, – этот список можно продолжать долго.
- Задача уменьшения размерности. На входе — признаки набора данных, на выходе – их меньше, они более эффективны, информативны и полезны для работы модели. Также алгоритм обучения без учителя (потому что нет готовых ответов, на которых можно обучать модель).
- Задача выявления аномалий. Напоминает задачу классификации, но отличие в том, что аномалии встречаются редко, однако имеют большое значение для системы (кибератаки, мошенничество с кредитными картами). На входе – набор признаков, которые могут быть самой разнообразной природы. На выходе, соответственно, ожидаются выявленные случаи аномалий. Если вам повезло и в вашем распоряжении имеются обучающие примеры, то это будет обучение с учителем. Но на практике чаще бывает, что подобных примеров нет.
⇡#Что такое логистическая регрессия?
Логистическая регрессия, как и линейная, была заимствована из статистики. Отличительной чертой логистической регрессии является то, что значением функции является вероятность. Вероятность чего? Закономерный вопрос. Давайте обо всем по порядку.
На входе логистическая регрессия, как и линейная, принимает одну или несколько независимых переменных (признаков набора данных) и подсчитывает их взаимосвязь с зависимой переменной. Различие в том, что логистическая регрессия применяет сигмоидную функцию (также известна как логистическая, или логит-функция), которая позволяет предсказывать непрерывную переменную со значениями на отрезке [0, 1] при любых значениях независимых переменных. Фактически это распределение Бернулли (для тех, кому это интересно).
Теперь наступает время ответить на вопросы, поставленные выше.
Логистическая регрессия вычисляет вероятность того, что данное исходное значение принадлежит к определенному классу. Она используется для задач классификации: оценивает апостериорные вероятности принадлежности данного объекта к тому или иному классу.
Для оценки модели логистическая регрессия применяет метод максимального правдоподобия. Он основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Попытаемся «на пальцах» сформулировать его принцип действия. Цель метода – оценить параметры распределения вероятностей. Способ – максимизировать функцию правдоподобия. Эта функция как раз определяет вероятность значений параметров регрессионной модели для заданного значения независимой переменной x=X:
P(θ)=P(x=X|θ),
где θ — значение параметра модели, P(θ) — вероятность появления значения θ, X — значение независимой переменной x, для которого определяется условная вероятность θ.
Задача заключается в поиске таких значений параметров Θ = (θ1, θ2,...,θn), которые максимизируют функцию правдоподобия L(x|Θ). Для этого определяются оценки максимального правдоподобия (maximum likelihood estimates), для которых значения параметров являются наиболее «правдоподобными» по отношению к наблюдаемым данным.
Если хочется еще больше математики, рекомендуем почитать про линейный дискриминант Фишера.
⇡#Линейная регрессия и логистическая регрессия: часто спрашивают на интервью сходство и различия
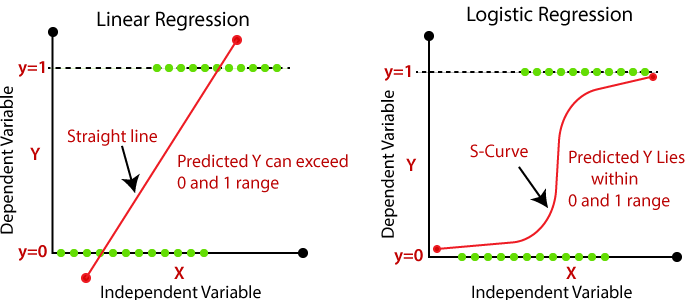
Оба этих алгоритма как альфа и бета машинного обучения и науки о данных. Посмотрим на их графики функций:
Сходство
Обе модели являются контролируемыми алгоритмами машинного обучения и используют линейные уравнения для прогнозов. Вот и всё сходство.
| Критерий сравнения | Линейная регрессия | Логистическая регрессия |
| Ввод – вывод | Ввод – независимая переменная (или несколько), вывод – прогноз зависимой переменной (задача регрессии) | Ввод – независимая переменная (или несколько), вывод – вероятность принадлежности к группе |
| Линия наилучшего соответствия | Прямая | Кривая |
| Способ минимизации ошибки | Метод наименьших квадратов | Метод максимального правдоподобия. |
| Результат на выходе | Вещественное число (прогноз изменений) | Число в интервале от 0 до 1. Можно осуществить бинарную классификацию: если число ниже порогового значения — то объект относится к 0 («нет»), а если выше — то к 1 («да») |
| Цель | Прогнозирование линейных трендов | Классификация (при добавлении соответствующего правила), но классификатором при этом не является |
⇡#Почему логистическая регрессия и какое нам до неё дело?
Во-первых, это отличный способ старта в машинном обучении. Возьмите любой курс машобуча и посмотрите, с чего он начинается. Скорее всего, это будет линейная, а затем логистическая регрессия. Дело в том, что они воплощают два главных метода обучения с учителем – классификацию и регрессию. Изучая эти два алгоритма, вы знакомитесь с основными понятиями, процессами и проблематикой машинного обучения, учитесь готовить данные к обработке, выбирать признаки, оценивать модель согласно различным метрикам (accuracy – доля правильных ответов, precision – точность, recall — полнота, F-measure – F-мера, ROC curve — кривая, Pearson correlation – корреляция Пирсона, mean squared error – корневая среднеквадратичная ошибка). Эти английские термины уже вошли в обиход, поэтому мы приводим их здесь. Отдельная статья о метриках машинного обучения планировалась в нашем цикле, пока не встретился вот этот отличный обзор.
Таким образом, можно изучить всё необходимое без сложной и нагроможденной архитектуры. Если вы потратите на это время, досконально разберетесь в линейной и логистической регрессии и напишете код, вам по плечу будут и мощные новейшие алгоритмы ИИ. И да, машобуч — это подмножество искусственного интеллекта. Массачусетский институт технологий также придерживается этой позиции.
Нейронные сети тоже вам покорятся, потому что каждый отдельный нейрон — своего рода логистическая регрессия. Искусственный нейрон имитирует работу живой нервной клетки, которая суммирует все входящие влияния, и если электрический потенциал суммы больше некоторого порога, то через принимающий нейрон будет распространяться потенциал действия («спайк»). Это же и есть бинарная классификация, где предсказываются 0 и 1, а в биологии этот принцип называется «все или ничего».
Поэтому часто оказывается, что логистической регрессии вполне достаточно для решения проблемы. Благодаря удобству интерпретации результатов, а также своей способности выявлять наиболее весомые, значительные признаки набора данных, ЛР успешно применяется, например, в финансах и бизнесе для оценки платежеспособности заемщиков, сегментации пользователей (приобретет – не приобретет товар или услугу), классификации текстов (спам – не спам, токсичный комментарий – не токсичный и т. д.), в медицине для оценки вероятности развития того или иного заболевания и для множества других задач. Обычно речь идет о бинарной классификации, однако в случае множественной (мультиномиальной) логистической регрессии зависимая переменная может иметь несколько категорий.
Этой информации должно быть достаточно, чтобы самостоятельно начать изучать логистическую регрессию. Рекомендуем использовать библиотеку scikit-learn и поэкспериментировать. Желаем успехов!
Другие материалы цикла:
- Искусственный интеллект: линейная регрессия и методы её обучения
- Искусственный интеллект: Генетический алгоритм и его применения
- Искусственный интеллект: алгоритмы поиска
- Хочу изучать искусственный интеллект!
- Отрасли и направления искусственного интеллекта: взгляд «с высоты птичьего полёта»
- Искусственный интеллект и сознание: imitation game
- Знакомство с искусственным интеллектом
Источники:
- Raschka S., Mirjalili V. Python machine learning: Machine learning and deep learning with Python, scikit-learn, and TensorFlow 2. – Packt Publishing Ltd, 2019. (Есть русский перевод этой книги).
- https://www.javatpoint.com/linear-regression-vs-logistic-regression-in-machine-learning