Квантовая коррекция ошибок: плод созрел?
Регулярно попадающие в информационные ленты сообщения о всё новых и ещё более многокубитных, чем прежние, квантовых компьютерах на деле раз за разом оказываются отчётами об успешных запусках лабораторных прототипов. Нет, формально всё честно, заявленные многие сотни кубитов работают как следует, — просто это физические кубиты, тогда как действительно полезные на практике вычисления придётся реализовывать на кубитах логических. А вот сколько первых пойдёт на создание одного-единственного второго, зависит от выбранного теми или иными исследователями метода коррекции ошибок; типичное на сегодня соотношение, как мы уже разбирали сравнительно недавно, — примерно 1000:1. Иными словами, из анонсированных к настоящему времени проектов разработки квантовых компьютеров, пожалуй, лишь детище канадского стартапа Xanadu, которое, как заявляют, к 2029 г. удастся масштабировать до 1 миллиона физических кубитов, сумеет обеспечить достаточную вычислительную мощь для взлома современных стойких шифров и решения иных прикладных задач. Да и то надежда эта пока представляется весьма эфемерной, — немалые подозрения вызывает сокрытие разработчиками самой важной компоненты обещанного успеха: взятого на вооружение механизма коррекции ошибок. В отсутствие же такого адекватного механизма даже формально работающие совместно тысяча логических кубитов сколько-нибудь приемлемого качества вычислений обеспечить не в силах. Адекватным же следует признать такой механизм, что будет гарантировать появление не более 1 ошибки на хотя бы 106 операций (больше — лучше) и в то же время окажется достаточно быстрым, чтобы произвести необходимые исправления за время, не превышающее длительности сохранения квантовой когерентности системы, — которое исчисляется пока в лучшем случае сотнями микросекунд.
Неудивительно поэтому, что основные усилия наиболее предусмотрительных разработчиков сосредоточены сегодня не столько на наращивании числа физических кубитов в системе, сколько на поисках значительно более эффективных способов коррекции ошибок. И определённый прогресс на этом направлении наблюдается: так, австрийские исследователи из Университета Инсбрука предложили в начале 2025-го использовать два кода коррекции ошибок вместо одного. В IBM же изобрели настолько удачный, по их заявлению, новый метод исправления вычислительных сбоев, что всерьёз намерены к уже упомянутому 2029 г. ввести в строй коммерческий квантовый компьютер Starling («Скворец») на 200 логических кубитов, а к 2033-му на его основе развить систему Blue Jay («Голубая сойка») — уже на 2000 логических кубитов. И вот тогда уже — пока-пока, RSA-шифрование, да и не оно одно: множество классических задач запретительной (в плане требуемых на их решение ресурсов) вычислительной сложности окажутся сняты с повестки дня. Возможно, как раз на подобные планы ссылался директор ФСБ России Александр Бортников, когда утверждал, что Пентагон в течение 5-10 лет хочет получить неоспоримое преимущество в сфере кибервойн, разработав на основе квантовых технологий инструмент, который обесценит все существующие системы криптозащиты.
Остаётся только понять: насколько обоснован оптимизм разработчиков — и удастся ли им на деле реализовать подлинно адекватный механизм коррекции ошибок для существенно многокубитных систем?

Схема межсоединений, связывающих физические кубиты в составе проектируемого IBM квантового процессора Loon, — наглядное свидетельство того, как геометрическая запутанность может оказаться под стать квантовой (источник: IBM)
⇡#Скворушка с проверками чётности
Анонсированный Google в конце 2024 г. квантовый вычислитель Willow с 105 физическими зарядовыми кубитами полагался, как и предыдущие устройства в этой серии, на поверхностный алгоритм коррекции ошибок, реализующий в данном случае схему d-7. Это позволило снизить частоту возникновения сбоев до 0,143% за каждый вычислительный цикл — и одновременно увеличить длительность сохранения системой когерентности примерно до 100 микросекунд. Важно также, что избранный исследователями подход — трансмоны в качестве физических кубитов, поверхностный алгоритм с поступательным наращиванием размерности при переходе к более масштабным системам — даёт возможность увеличивать продолжительность сохранения когерентного состояния логического кубита даже в том случае, когда длительность сохранения когерентности физическими кубитами остаётся неизменной. То бишь чем крупнее организуемый по такой схеме квантовый вычислитель, тем дольше и точнее он будет работать.
Другое дело, что для вывода погрешности вычислений — т. е. вероятности ошибочного исполнения одиночной арифметической или логической операции вычислительным контуром — на уровень хотя бы 10−6 (1 ошибка на 1 миллион операций) потребуется реализовать поверхностный алгоритм по схеме d-27, что подразумевает эмуляцию одного логического кубита примерно полутора тысячами физических. Для сравнения: современные полупроводниковые процессоры допускают в худшем случае одну вычислительную ошибку за месяц непрерывной работы, что позволяет оценить соответствующую вероятность в 10−13...10−15 для единичной операции. Понятно, что с инженерной точки зрения стоящая перед разработчиками квантовой коррекции ошибок задача чудовищно сложна. Не говоря уже о том, что сами логические кубиты, полученные в итоге этого исполинского труда, придётся ещё неким образом организовывать в квантово запутанную систему, чтобы решать прикладные задачи уже на существенно многокубитном компьютере. Причём вопросом, каким именно образом это делать, исследователи из Google предметно пока даже не задавались.
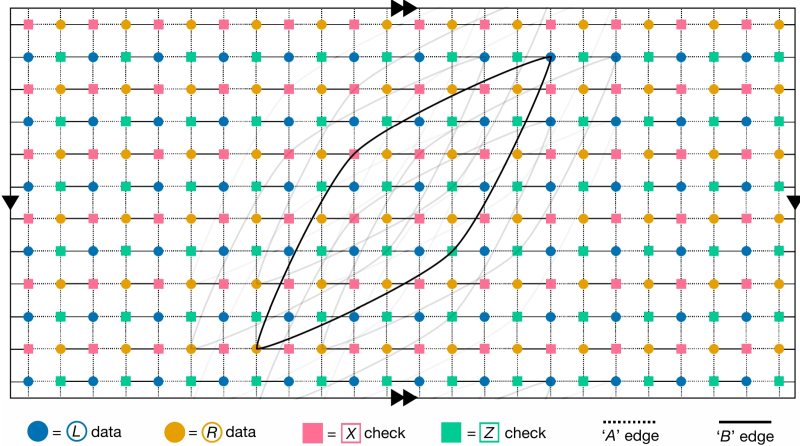
Граф Таннера (двудольный граф, применяемый для визуализации алгоритмов коррекции ошибок) для предложенного IBM Quantum кода с низкоплотной проверкой чётности иллюстрирует исправление сразу двух типов ошибок, битовых (X) и фазовых (Z), — иллюстрация из работы High-threshold and low-overhead fault-tolerant quantum memory, https://doi.org/10.1038/s41586-024-07107-7 (источник: IBM)
Подход их коллег из IBM в этом смысле принципиально иной: хотя те изначально тоже рассматривали поверхностный алгоритм как оптимальный метод коррекции ошибок, довольно быстро был сделан вывод, что громоздкость получаемой в результате физической конструкции ощутимо обесценивает обеспечиваемые поверхностным алгоритмом преимущества. Вице-президент IBM Quantum Джей Гамбетта (Jay Gambetta) прямо назвал создание адекватной материальной структуры для реализации поверхностного алгоритма с высокими размерностями (вроде упомянутой d-27) «инженерными грёзами» (engineering pipe dream), так что начиная с 2019 г. разработчики из этой компании ориентируются на другой, более приземлённый алгоритм — на низкоплотную проверку чётности для квантовых систем; quantum low-density parity check (qLDPC). Утверждается, что использование этой схемы вместо поверхностного алгоритма позволит сократить число физических кубитов, необходимых для реализации одного логического, примерно на порядок, так что уже в 2026-м IBM планирует явить миру 12-кубитный квантовый компьютер, построенный на 288 физических кубитах и производящий вычисления с погрешностью не более 0,1%. Для сравнения: аналогичный вычислитель, но организованный по схеме поверхностного алгоритма, потребовал бы для формирования той же дюжины логических кубитов и достижения схожей погрешности примерно 3 тыс. физических кубитов.
Принципиальное отличие схем коррекции qLDPC от поверхностного алгоритма — в том, что последний полагается на сравнение состояний соседних физических кубитов, тогда как первые связывают разнесённые в пространстве кубиты транслирующими квантовые состояния сцепками (couplers), организуя тем самым «нелокальные» взаимодействия между элементами квантовой системы. Ещё до конца 2025 г. планируется завершить воплощение «в металле» квантового процессора Loon («Гагара»), который как раз и станет предметным воплощением qLDPC-архитектуры с «нелокальными» сцепками. Задача эта технически нетривиальная: чем больше расстояние между квантовыми макроустройствами, тем сложнее реализовать механизм их запутывания — и поддерживать его на протяжении времени, достаточного для произведения собственно вычислений. В 2026-м на смену «Гагаре» должна явиться «Кукабарра» (Kookaburra) — первый в практике IBM модульный квантовый процессор, комбинирующий квантовую память с логическими контурами для проведения операций над данными. Именно такая система, а не условный «квантовый сумматор» (просто арифметически-логическая схема, без подсистемы хотя бы временного хранения) и станет основой для построения в дальнейшем отказоустойчивых многопроцессорных квантовых компьютеров. Напомним на всякий случай, что и Google Willow, и выводимые IBM «пташки» — Loon и Kookaburra — представляют собой одночиповые системы. Для решения же практических задач, включая пресловутый взлом супернадёжных ныне криптоалгоритмов, потребуются именно многопроцессорные вычислители: разместить на одной подложке ни пару сотен, ни тем более пару тысяч логических кубитов возможным на данный момент не представляется. Именно поэтому в дальнейших планах IBM Quantum — построение в 2027 г. системы «Какаду» (Cockatoo) из пары «Кукабарр», соединённых линейными сцепками (L-couplers), которые призваны обеспечить квантовое запутывание уже на межпроцессорном уровне. В 2029-м же в строй должен войти «Скворец», Starling, — коммерчески доступный через облако квантовый компьютер на 200 логических кубитов; венец и промежуточный итог обкатанных на всех предыдущих представителях этого «птичника» инженерных решений.

Так, по замыслу разработчиков, в 2029 г. будет выглядеть развёрнутый в машинном зале коммерческий квантовый вычислитель Starling (источник: IBM)
Нарисованная представителями IBM Quantum перспектива более чем впечатляет: ещё бы, всего каких-то четыре года (даже меньше: Starling должен быть полностью готов уже в 2028-м, просто перед открытием к нему доступа через облако компьютер намереваются интенсивно испытывать сами разработчики) — и в распоряжении человечества окажется двухсоткубитный квантовый вычислитель. Правда, оговариваются эксперты, чтобы выдержать столь высокие заявленные темпы, инженерам придётся быстро и эффективно решить целый ряд не самых тривиальных проблем. Для начала — на уровне прикладной микроэлектроники: уже для изготовления чипов Loon потребуется организация существенно трёхмерной полупроводниковой структуры. Не просто слоистой с колодцами-vias, бесхитростно пронизывающими всю стопку плоских базовых микросхем, — как в случае 3D-памяти, скажем, — а по-настоящему сложно организованной, когда одна непрерывная линия сцепки прихотливо прошивает несколько горизонтальных слоёв в определённой последовательности, частично продолжаясь в заданных ими плоскостях и снова уходя по вертикали вверх или вниз. К счастью, технологические нормы, по которым изготавливают полупроводниковые (точнее, трансмонные) квантовые процессоры, достаточно крупномасштабны, чтобы в крайнем случае столь изощрённую трёхмерную систему можно было выполнять методами безмасочной литографии, допускающими едва ли не ручной контроль, — воздействием электронных пучков, скажем.
Следующая загвоздка, с которой предстоит разбираться инженерам, — это достоверность срабатывания квантовых вентилей; gate fidelity. Дело в том, что очень долгое время исследователи были сосредоточены на получении собственно кубитов — макроскопических квантовых объектов, над которыми (когда-нибудь, в перспективе) можно будет производить различные операции. И вот по мере того, как разные технологии получения кубитов, включая обсуждаемые здесь трансмоны, становились совершеннее, на первый план начала выступать другая проблема, а именно — произведение над более-менее готовыми к эксплуатации кубитами логических операций. Для обычных битов (на практике — порций электрического заряда в классических микросхемах) средствами произведения таких операций служат логические вентили — контуры, преобразующие входные битовые величины в выходные по правилам булевой алгебры: AND, CNOT, XOR и т. д. Квантовыми же вентилями называют фундаментальные операции, преобразующие состояния кубитов — тоже по определённым правилам, что в какой-то мере соответствуют формально-логическим, но неизбежно учитывают необходимость менять разом состояние всей квантовой системы, находящейся, напомним, в суперпозиции до самого момента измерения. Важность замечания «в какой-то мере» наглядно поясняет следующий факт: до тех пор, пока не произведено измерение состояния квантовой системы, квантовые вентили полностью обратимы, т. е. прохождение через вентиль сигнала в обратную сторону восстанавливает состояние кубита (или кубитов), каким оно было до момента применения данного вентиля. Исходя из этого, кстати, уже понятно, что квантовые алгоритмы должны существенным образом отличаться от классических, и что уже по одной этой причине область применения квантовых компьютеров серьёзно ограничена. Там, где они потенциально превосходят классические (а это как раз по большей части задачи с выбором одного верного решения из сонма неверных — факторизация чисел, задача коммивояжёра и т. п.), превосходство это с появлением тысячекубитных вычислителей окажется подавляющим. Там же, где квантовые алгоритмы неприменимы, без привычных фоннеймановских компьютеров и двадцать лет спустя не удастся обойтись.
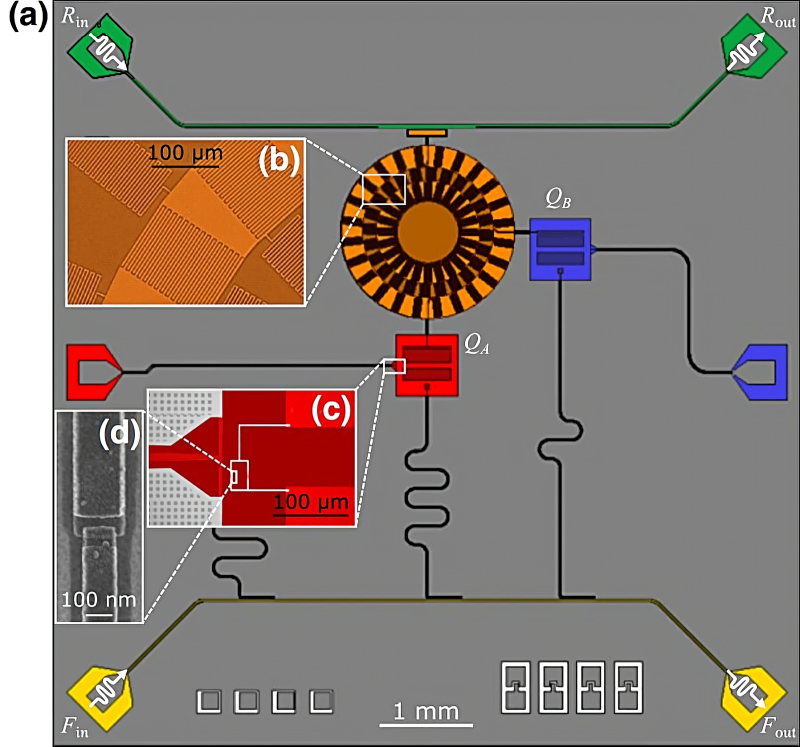
Один из вариантов дизайна двухтрансмонной квантовой сцепки: (a) — общая схема контура с кольцевым резонатором на основе метаматериала; (b) и (c) — оптические микрофотографии элементов устройства с выделением рабочих зон в псевдоцветах; (d) полученное на сканирующем электронном микроскопе изображение джозефсоновского перехода в кубите. Сцепка сформирована парой трансмонных кубитов, 𝑄𝐴 и 𝑄𝐵, связанных с кольцевым резонатором (источник: PRX Quantum)
Так вот, достоверность срабатывания как раз и является той мерой, что определяет различие между результатом применения данного конкретного физического вентиля — и тем, что продемонстрировал бы аналогичный идеальный вентиль в отсутствие каких бы то ни было погрешностей. А погрешностей таких в реальной системе с макроскопическими квантовыми объектами по самым объективным причинам накапливается множество, от воздействия теплового движения молекул образующего кубиты вещества до влияния космических лучей (последние, кстати, и в классические вычисления на полупроводниковых процессорах дополнительные ошибки способны вносить). В конце 2024 г. японские исследователи из Центра квантовых вычислений RIKEN и профильной лаборатории Toshiba отчитались о создании высокодостоверной двухтрансмонной сцепки (double-transmon coupler, DTC) — необходимого элемента квантовой системы того рода, к которому относится пестуемый в IBM Quantum «птичник». Но что значит — высокодостоверной? Показатель её gate fidelity для однокубитных вентилей составил, по заявлению японской группы, 99,98%, а для двухкубитных — 99,90%. Выходит, надёжность квантовых вычислений даже с применением одной-единственной DTC вновь замирает на уровне 10−3, и чем больше операций подразумевает квантовый алгоритм, тем выше будет становиться вероятность получить неверный ответ. К счастью, тем квантовая вычислительная система и хороша (в приложении к специфичному для неё кругу задач), что выдаёт ответ практически мгновенно, просто фиксируя по итогу измерения своё состояние. И чтобы удостовериться в корректности полученного результата, достаточно одну и ту же задачу прогнать на том же самом квантовом компьютере хотя бы два раза, а лучше три, — если ответы в целом совпадут, с крайне высокой точностью можно принимать их на веру. Но если требуется, к примеру, взломать 1024-разрядный ключ шифрования, а результатом оказывается число, определённое с точностью всего лишь 10−3, работу дешифровальщиков это, бесспорно, облегчит, но всё-таки совсем уж скучать их не заставит.
В IBM Quantum надеются, что надёжность вычислений на их «птичьих» системах в ближайшие годы может быть увеличена по меньшей мере на один десятичный порядок величины, — уже это позволит реализовывать на уровне Cockatoo избранные квантовые алгоритмы с приемлемой на практике точностью. Важнейшая предпосылка к дальнейшему повышению достоверности — увеличение времени когерентности квантовой системы: грубо говоря, чем дольше поддерживается состояние квантовой запутанности, тем больше шансов отыскать и исправить накапливающиеся в ходе вычислений ошибки. И если для «Цапель» (Heron), квантовых чипов IBM предыдущего поколения, полагавшихся ещё на поверхностный алгоритм коррекции, типичная продолжительность когерентности не превышала 150-200 микросекунд, то в случае Loon этот показатель удалось улучшить до 2 миллисекунд. Правда, пока только для хорошо изолированной тестовой системы: внутри работающего над реальными задачами компьютера, по соседству с другими аналогичными квантовыми процессорами и электронными цепями обвязки, удерживать когерентность удаётся на заметно меньшем интервале. Тем не менее «птичник» рассматривается как чрезвычайно перспективное направление: да, выбранная схема коррекции ошибок qLDPC громоздка в плане физического воплощения и подвержена внешним воздействиям, однако все возникающие из-за этого сложности заведомо компенсируются резким сокращением числа физических кубитов, необходимых для реализации одного логического.
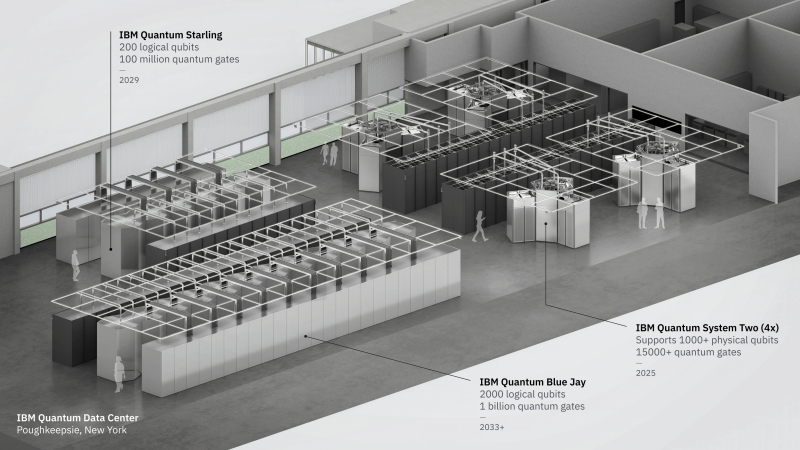
Рендер, на котором наглядно продемонстрированы габариты действующего квантового компьютера Quantum Two в сравнении с проектируемыми системами Starling и Blue Jay (источник: IBM)
Особенно же воодушевляет разработчиков квантовых систем (и заставляет грустнеть криптографов) тот факт, что корректировать ошибки в подобного рода системах можно довольно значительным количеством способов — не обязательно даже чисто аппаратных. Так, в Университете МИСИС создали самообучающийся инструмент для поиска и исправления ошибок на основе нейросетей — работающий, что неудивительно, тем лучше, чем больше в системе кубитов (т. е. чем обширнее база для тренировки модели). В этом случае применение нашли рекуррентные нейронные сети, анализирующие временные ряды, данные для которых, в свою очередь, поступают в результате измерения состояний вспомогательных (контрольных) физических кубитов в составе логических. Отдельно подчёркивается такое преимущество инструмента, как приспособление его к каждому конкретному квантовому компьютеру с «усвоением» (на уровне весов на входах перцептронов нейросети) присущих именно тому особенностей работы.
Другой оригинальный подход применили разработчики из Amazon, которые при создании нового квантового процессора Ocelot сделали ставку на гибридную архитектуру — сведя в едином устройстве привычные уже трансмонные кубиты с так называемыми кошачьими (cat qbits, — отсылка к пресловутой кошке Шрёдингера), априори более устойчивыми к одному из двух ключевых типов ошибок, которым подвержены квантовые вычислительные системы, а именно к «перевороту бита»; bit-flip. Кошачьи кубиты опираются в качестве элементарных квантовых систем на фотоны, а не на электроны, и, поскольку мощность когерентного фотонного пучка (т. е. лазера) может быть с лёгкостью усилена, случайный «переворот фазы» одиночного фотона в таком пучке состояния квантового объекта в целом — группы фотонов в данном случае — не изменит. А для коррекции ошибок другого типа, phase-flip, окажется достаточно пары запутанных с кошачьим кубитом трансмонов. Да, конструкция выходит довольно громоздкой и энергоёмкой, но зато длительность когерентности такой гибридной системы достигает, по заявлениям Amazon, целой секунды, а число необходимых для реализации одного логического кубита физических снижается разом едва ли не на порядок. В итоге разработчики надеются сократить время вывода на рынок устойчивого к ошибкам и практически применимого к реальным задачам квантового компьютера по меньшей мере на пять лет. Анонс Ocelot пришёлся на начало 2025 г. — значит, если считать за прежний срок появления такого компьютера 2033-й (предположительная дата вступления в строй IBM Blue Jay), криптографам следует срочно переходить на квантово-стойкие алгоритмы уже к 2028-му, не позже.
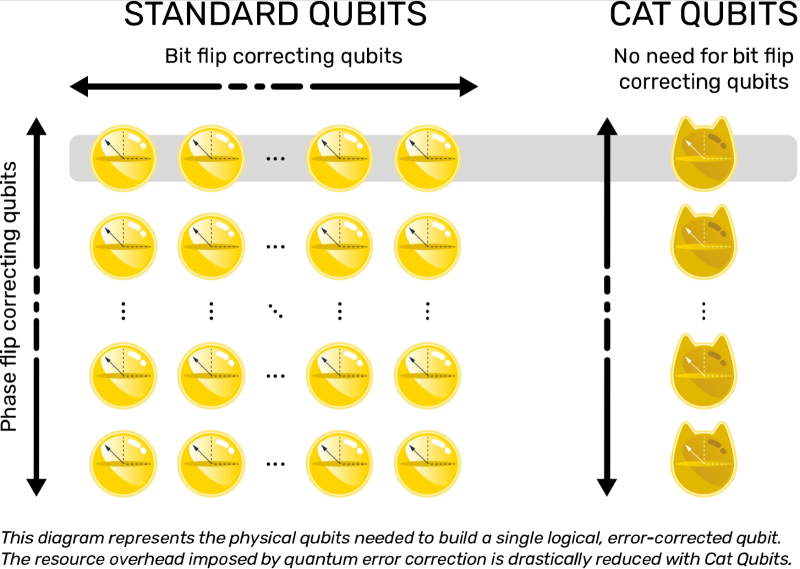
Схема, поясняющая преимущество кошачьих кубитов перед трансмонами: слева — кубиты, подверженные квантовым ошибкам обоих типов; справа — кошачьи (ушки добавлены для наглядности), которые нуждаются в коррекции только phase-flip (источник: Alice and Bob)
Разработка квантовых компьютеров за последний буквально год объективно ускорилась — в немалой степени как раз по причине появления сразу нескольких методов эффективной коррекции ошибок. Вот уже и вездесущая Nvidia объявила о намерении открыть в Бостоне профильный исследовательский центр, и в КНР создали универсальный блок контроля и управления для систем со сверхпроводящими кубитами, совместимый практически с любой платформой такого типа и готовый оперировать 1 тыс. (физических) кубитов изначально, а в перспективе, послед модернизации, — и 5 тыс., и даже 10 тыс. Важно, что такое устройство представляет собой полностью суверенную разработку, что даёт КНР возможность независимо конкурировать с разработчиками квантовых компьютеров из других регионов мира. В то же время запущенный в середине 2025 г. в Японии крупнейший в мире квантовый компьютер на 256 сверхпроводящих кубитах во многом схож с американскими разработками по тому же самому направлению — что, с одной стороны, позволяет заимствовать уже отлаженные решения, а с другой — сужает возможности для творческого манёвра идеями.
IBM же, в свою очередь, совместно с AMD планирует развивать «квантово-центричные супервычисления» — масштабируемые платформы, в составе которых квантовые компьютеры должны трудиться совместно с высокопроизводительными фоннеймановскими серверными кластерами, реализующими в том числе ИИ-вычисления. Для внешнего пользователя, таким образом, цельная система будет представляться неким чёрным ящиком, который каждую предложенную ему задачу будет решать оптимальным для той способом — и на наиболее подходящей аппаратной основе. Причём в выигрыше от перехода на такие системы окажутся не только гиперскейлеры, серверам которых приходится одновременно исполнять множество разнородных вычислений, но и клиенты нового типа. А именно — такие, которые станут активно применять для решения новых задач комбинированные алгоритмы, подразумевающие частью классические, частью квантовые вычисления, а частью и ИИ-инференс. Собственно, пока что таких «квантово-центричных супервычислений» не производится ровно потому, что нет для этого подходящей основы. Но едва та появится — кто знает, какие задачи поставят перед небывалыми прежде системами пытливые умы? И поскольку в отсутствие эффективной коррекции ошибок для квантовых компьютеров в тысячи логических кубитов подобные супервычисления невозможны в принципе, можно надеяться, что как раз в конце текущего — начале следующего десятилетия вычислительная математика откроет для себя (а заодно и для человечества) совершенно новые горизонты.
