⇣ Содержание

|
Опрос
|
реклама
Самое интересное в новостях
Базовые принципы нейрокомпьютинга, или Почему параллелизм важнее скорости
Компьютеры классической архитектуры фон Неймана оптимальны для последовательного решения задач. Потенциально — если проблема сводится к строго прямолинейному исполнению цепочки элементарных операций (с возможным включением циклов) — быстрота получения результата ограничивается лишь физическими возможностями элементной базы, на которой реализована данная фоннеймановская машина. Человеку с ней тягаться бессмысленно: это доказали уже довольно давно победы компьютера над живым гроссмейстером сперва в шахматах, а после и в игре го, каждая партия которых по сути сводится к последовательному перебору допустимых ходов со средне- и долгосрочной оценкой их оптимальности. 
В 2020 г. в Массачусетском технологическом институте создали прототип нейроморфного (то есть функционирующего по тем же принципам, что и человеческий мозг) чипа на основе мемристоров (источник: MIT) Однако есть целый набор классов задач, которые принципиально не сводятся к последовательному перебору. Образно их можно классифицировать как «опознание ранее не виденного на основе знания об уже известном». Взять хотя бы анализ изображений: мы настолько привыкли не осознавать высочайшее качество своей способности распознавать образы предметов даже на плоскости (не говоря уже о трёхмерной сцене), что оптические иллюзии или «невозможные картины» в духе Эшера приводят нас в лёгкое замешательство. Для фоннеймановского же компьютера любое изображение — фото ли это котёнка, трёхмерная развёртка тессеракта или бесконечная лестница Пенроуза — просто мешанина пикселей. Причём универсального алгоритма для поиска какого-либо подобия упорядоченности в этой мешанине не существует; решать такие задачи приходится в полном смысле слова численными методами. Важно, что прикладных вычислительных задач, избыточно сложных для классических компьютеров, становится тем больше, чем глубже технологии проникают в повседневную жизнь, экономику, науку и даже политику. Распознавание и генерация речи в реальном времени, точное (то есть с заведомо ничтожной долей ложных срабатываний в обе стороны) отождествление человека по лицу, предсказание развития биржевых трендов, определение богатых на полезные ископаемые участков по снимкам из космоса, прогностическая оценка поведения сложных систем, включая политико-экономические, — буквально тысячи их. 
Литография «Восхождение и спуск» Маурица Эшера (Maurits Cornelis Escher) демонстрирует визуальную иллюзию — «невозможную лестницу», четыре пролёта которой замкнуты в бесконечную спираль (источник: Wikimedia Commons) Компьютерам сегодня необходимо научиться эффективно решать существенно параллельные задачи, с применением нечёткой логики и в условиях острой нехватки входящей информации. Банальным повышением рабочих частот классических процессоров с одновременным наращиванием плотности транзисторов на каждый их квадратный миллиметр справиться с этим не выйдет. Гораздо логичнее взять за основу биологический мозг — и если не воспроизвести его работу один к одному, то хотя бы создать вычислительную систему на схожих принципах. Ну или эмулировать работу такой системы на очень мощных фоннеймановских машинах или кластерах (сетях), состоящих из подобных машин. Другой вопрос: а что это, собственно, за принципы? ⇡#Выделения в коре: как работает мозгОсновную вычислительную — мыслительную — работу в случае биологического организма, если говорить о млекопитающих в целом, исполняет кора головного мозга. У человека она в среднем содержит 16 млрд нейронов — базовых логических вычислительных узлов аналогового типа. Каждый из этих нейронов опять-таки в среднем соединён отростками примерно с 10 тыс. других. Как именно с биологической точки зрения реализована обработка информации внутри нейрона — вопрос особый, но для целей нашего сегодняшнего материала принципиально несущественный. 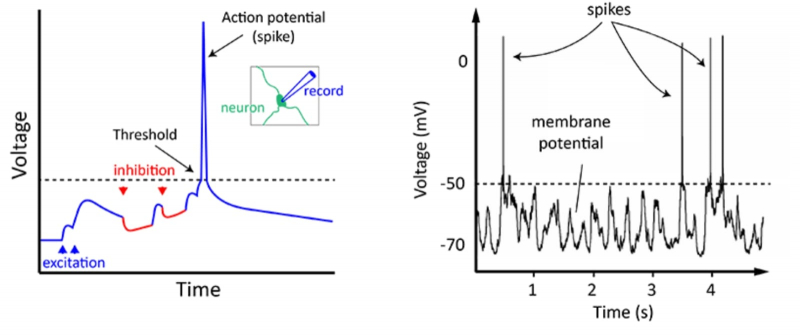
Слева: формирование потенциала действия (пика напряжения, выходящего далеко за пороговый уровень) в нейроне в ходе взвешенного суммирования возбуждающих и тормозящих сигналов от дендритов. Справа: составленный из отдельных пиков пакет потенциалов действия, распространяющийся по аксону (источник: The University of Queensland) Главное, что нейрон получает множество сигналов по разветвлённой системе входных терминалов, отростков примерно микронной толщины, называемых дендритами. Далее внутри — в теле, или соме, клетки — он производит их взвешенное суммирование. При достижении определённого порога накопленного таким образом стимула нейрон активируется, генерируя на единственном своём выходном терминале — покрытом изолирующей миелиновой оболочкой отростке, аксоне, — электрический импульс. Этот импульс, именуемый потенциалом действия, представляет собой серию краткосрочных (порядка 1 мс с интервалом между пакетами ~200 мс) всплесков напряжения примерно по 60 мВ каждый. На дальнем от сомы конце аксона располагается синапс — особый контакт, посредством которого выходной сигнал передаётся на дендрит другого нейрона. Особенность структуры биологического мозга заключается в том, что взаимодействие между её элементами — не чисто электрическое, как в полупроводниковом чипе, а электрохимическое. Синапс — вовсе не банальный проводник сигнала между аксоном и дендритом: под влиянием потенциала действия (одного или в ряде случаев нескольких) он выделяет определённые молекулы, нейротрансмиттеры, которые диффундируют в солевом растворе, заполняющем узкую щель между синапсом нейрона-источника и клеточной мембраной дендрита нейрона-приёмника. 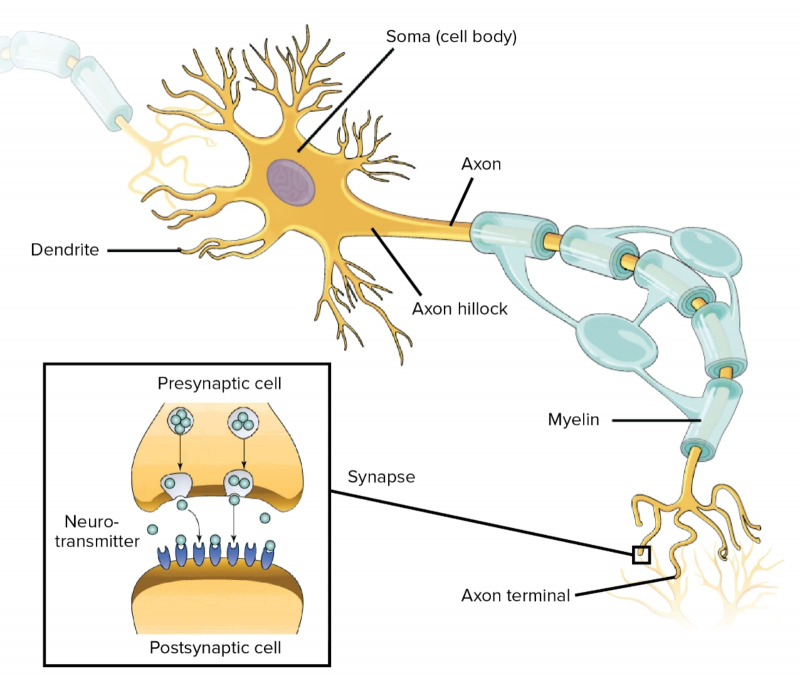
Главные компоненты нейрона и (на врезке) схема организации передачи сигнала в синаптической щели: сверху — аксонный терминал, снизу — окончание дендрита (источник: Khan Academy) Нейротрансмиттеры связываются с комплементарными им молекулами-рецепторами на контактной поверхности дендрита и стимулируют тот к открытию ворот проводимости, через которые проходят заряженные частицы — ионы. И вот уже эти ионы меняют электрический потенциала дендрита, провоцируя распространение по нему (точнее, по заполняющему его трубчатую внутренность солевому раствору) электрического импульса в направлении сомы нейрона-приёмника. Картину усложняет то, что каждый дендрит в данный момент времени способен испытывать воздействие от множества синапсов; что величина генерируемого в дендрите импульса зависит от числа открытых ворот проводимости, которое в свою очередь определяется количеством испущенных синапсами нейротрансмиттеров. Еще одну переменную в уравнение добавляет то, что одни синапсы стимулируют дендриты, с которыми взаимодействуют, — а другие, напротив, тормозят генерацию в них электрического импульса. 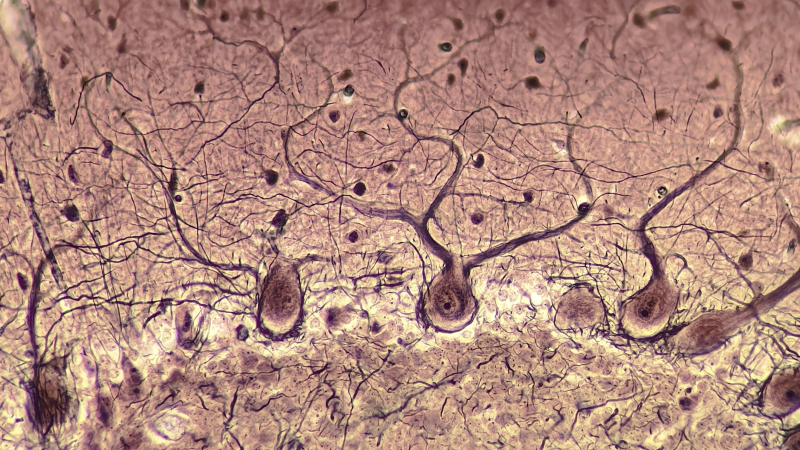
Микрофотография открытых Яном Пуркинье (Jan Purkyně) в 1839 г. «ганглиозных телец»: расположенных в мозжечке крупных нейронов с чрезвычайно разветвлёнными дендритами (источник: Wikimedia Commons) И хотя аксон у каждого нейрона один, синаптических выходов на нём может быть несколько, что дополнительно увеличивает связность и комплексный характер функционирования мозга как сети генерации, модуляции и передачи сигналов, а главное — как способной к обучению сети. ⇡#Простота хужеИсполнить готовый алгоритм для решения некой задачи и обучиться её решать — принципиально разные подходы. По первому пути идут фоннеймановские компьютеры, безвольные исполнители созданных биологическими программистами алгоритмов. По второму — нейронные сети, в определённом приближении воспроизводящие структуры коры головного мозга тех же самых биологических программистов. Правда, как и человеку, нейронной сети свойственно ошибаться, но ведь и программы для фоннеймановских машин несовершенны — без регулярного выпуска патчей, исправляющих огрехи функциональности и безопасности, не работает никакое современное ПО, созданное опять-таки пресловутыми биологическими программистами (про NoCode/LowCode разговор особый). 
Хотя художник изобразил Mariner 1 летящим меж звёзд, через 290 с после старта ракета-носитель с этим аппаратом была подорвана по команде с Земли из-за допущенной ошибки в коде (источник: NASA) Природа ошибок, неизбежно возникающих в сколько-нибудь объёмистом программном коде, чисто человеческая: невнимательность, недостаточная продуманность логических конструкций, банальные опечатки. Известны спровоцированные подобными ошибками громкие катастрофы: так, первый запуск к Марсу американского корабля Mariner 1 в 1962 г. оказался неудачным — стартовый расчёт был вынужден через пять минут после взлёта ракеты-носителя отдать ей команду на самоликвидацию, чтобы не допустить неконтролируемого уклонения от курса. А всё потому, что при вводе в бортовой компьютер написанного от руки кода оказался пропущен не слишком чётко читавшийся в рукописи дефис. «Самый дорогой дефис в истории», как назвал его позже Артур Кларк (Arthur C. Clarke), обошёлся в 80 млн тогдашних долларов (почти 745 млн в ценах 2022-го) — примерно 7 % всего бюджета, выделенного NASA на тот год. Обучение, разумеется, не служит гарантией безошибочного принятия решений — но по крайней мере от багов на уровне кода (за полным отсутствием такового) нейронная сеть будет избавлена. Главное — добиться того, чтобы её элементы действовали хотя бы примерно в соответствии с принципами работы биологических нейронов. И на первых порах, когда нейробиологи имели ещё весьма смутное представление о работе самих этих нервных клеток, искусственный нейрон представлял собой довольно грубое подобие натурального. 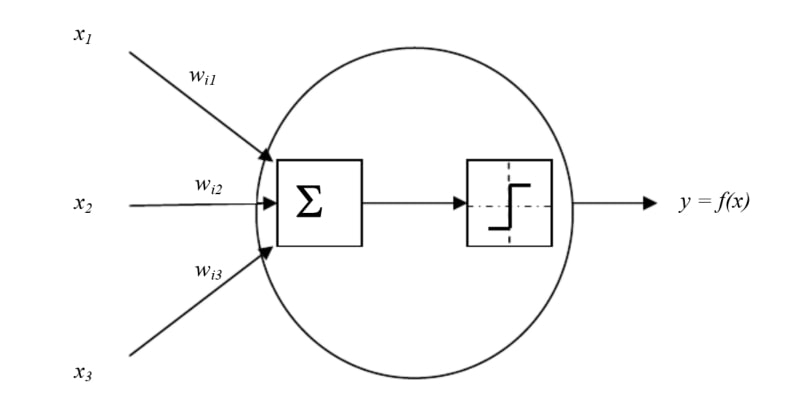
Модель искусственного нейрона Маккаллока — Питтса: входящие сигналы x1..x3 модулируются жёстко заданными весами wi1..wi3, после чего производится суммирование (Σ). Полученная величина сравнивается с установленным порогом срабатывания, и если она его превышает, происходит выдача результирующего сигнала y=f(x) (источник: Research Gate) Речь идёт о модели Маккаллока — Питтса, предложенной ещё в 1944 году и названной так по именам её авторов — нейрофизиолога и одного из основателей кибернетики как науки Уоррена Маккаллока (Warren McCulloch) и увлекавшегося математической логикой лингвиста Уолтера Питтса (Walter Pitts). Это, по сути, пороговый множественный сумматор: на его вход поступает несколько сигналов «истина» или «ложь» с определёнными весами, и если их сумма превышает некое заранее заданное пороговое значение, то на единственный выход сумматора подаётся значение «истина», иначе — «ложь». Это действительно похоже в первом приближении на работу биологического нейрона, по аксону которого не проходит импульс до тех пор, пока вся совокупность сигналов от дендритов не превзойдёт некоторого порога. Более того, из подобных искусственных нейронов можно, устанавливая различные пороговые значения их срабатывания, выстраивать базовые логические вентили — «логическое И», «логическое ИЛИ», «логическое НЕ» и более сложные. Чем, казалось бы, не электронный мозг? 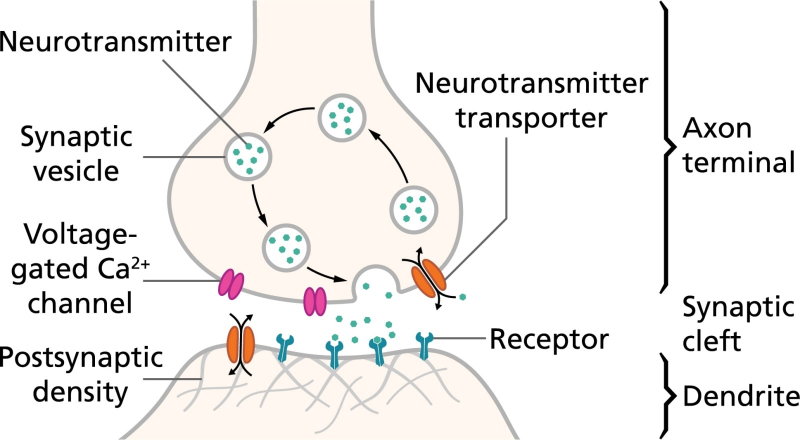
Активация биологического нейрона через синаптическую щель реализуется сложным образом, позволяющим химическим путём регулировать силу формируемого в дендрите сигнала, что соответствует переменным синаптическим весам, которых модель Маккаллока — Питтса не предусматривает (источник: The University of Queensland) Однако у модели Маккаллока — Питтса, если применять её для эмуляции мозговой деятельности, есть критический недостаток: она не позволяет построенной на основе искусственных нейронов системе обучаться. Не позволяет потому, что веса входящих сигналов в этой модели жёстко фиксированы, а значит, воздействие на систему того или иного фактора всякий раз будет оказываться однотипным. Обучение же построено на переосмыслении полученного опыта: ребёнок тянется ко всему яркому и тёплому, но стоит ему один раз коснуться пальцем огня — и больше не придётся объяснять, почему этого нельзя делать. Образ пламени в нейронах его мозга (как именно он там будет закодирован в виде электрических импульсов, здесь не существенно) получит огромный отрицательный вес, и команды «протянуть руку к этому-вот-яркому-тёплому» станут надёжно блокироваться. По крайней мере до наступления бунтарского пубертатного возраста. ⇡#Учиться, учиться и ещё раз учитьсяСледующим приближением к моделированию биологического нейрона стал предложенный несколько позже, в 1957-м, психологом и нейрофизиологом Фрэнком Розенблаттом (Frank Rosenblatt) перцептрон (от англ. perception, «восприятие») — искусственный нейрон с переменными весами на каждом из входов. Именно благодаря тому, что веса переменные, а не заданные с самого начала конструктором нейронной сети, появляется возможность менять значения этих самых весов в зависимости от того, какой результат выдаёт перцептрон, — и тем самым реализовывать процесс обучения. 
Фрэнк Розенблатт рядом с действующей моделью своего перцептрона (источник: Cornell University Library) Перцептрон принципиально имеет дело с сигналами и, более того, весами различных знаков: положительные соответствуют усилению (возбуждению) стимула в биологическом нейроне, отрицательные — его торможению (ингибированию). Модулированные синаптическими весами входные сигналы поступают на сумматор перцептрона, а затем эта взвешенная сумма сравнивается с заранее заданной пороговой величиной: если первая меньше второй, искусственный нейрон Розенблатта остаётся в состоянии покоя, если больше — генерирует на выходе импульс. Уже эта сравнительно несложная конструкция позволяет небиологическим структурам воплощать базовые когнитивные функции, такие как распознавание образов. При этом никаких алгоритмов перцептрону не требуется: достаточно снабдить его значительным (в пределе — бесконечным) объёмом обучающего материала. Схема же самого обучения такова: a) изучаемый объект обследуется некими датчиками (которые могут считывать то же изображение попиксельно либо выделять в нём некие характерные формы и свойства), b) каждому из входов перцептрона случайным образом присваивается некий малый по модулю вес, c) производится взвешенное суммирование сигналов с входов и формируется отклик перцептрона («есть сигнал — нет сигнала», «да — нет»), d) экспериментатор получает ответ и сравнивает с исходным изображением: если перцептрон сработал верно, переходит к следующему объекту, а вот если нет... e) то веса на входах корректируются с учётом величины ошибки, и процедура повторяется с самого начала. 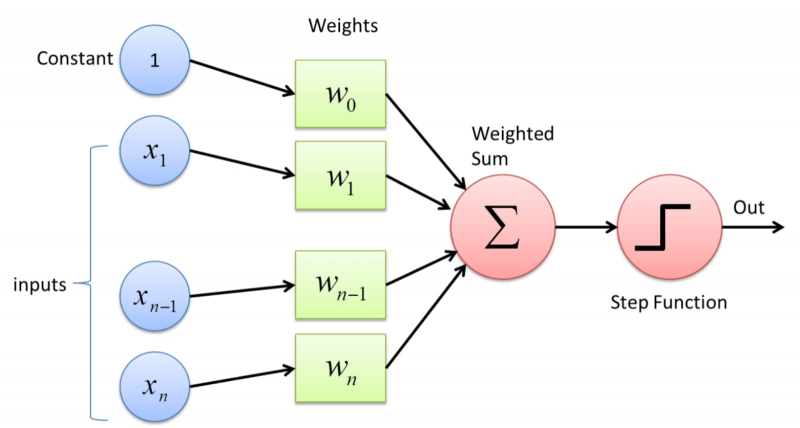
На входы перцептрона подаются константы, сигналы от внешних датчиков или иных перцептронов и значения весов, после чего производится взвешенное суммирование и активация выходного потенциала по заданному закону (источник: Towards Data Science) С точки зрения логики перцептрон — классический «чёрный ящик», поскольку в общем случае экспериментатор не контролирует вручную перераспределение весов после каждого ошибочного акта распознавания. Он просто сообщает машине, что та сработала неверно. Понятно, что в ряде случаев некоторое предпрограммирование перцептронов возможно и даже разумно: к примеру, если машине необходимо выделять в потоке людей тех, кто идёт без медицинской маски, отрицательный вес признака «наличие маски на лице» заведомо будет огромным, подавляющим по отношению ко всем прочим. ⇡#В сетях познанияОднако к исходу 1960-х стало ясно, что одного перцептрона недостаточно. Да, модель Розенблатта уверенно справляется с различением сущностей, между которыми можно провести чёткую границу «да — нет»: отличает кошку от собаки, розу от пиона, мотороллер от мопеда и так далее. Особенно хорошо работают несколько перцептронов вместе, в едином, если так можно выразиться, слое восприятия: каждый фокусируется на распознавании какого-то отдельного свойства или характеристики изучаемых машиной объектов. Но всё-таки возможностей одиночного слоя искусственных нейронов, сколько бы их там ни было, недостаточно, чтобы реализовать такую ключевую для математической логики функцию, как «исключающее ИЛИ». А ведь для формирования когнитивной функции она играет важнейшую роль и в повседневной жизни используется нами, биологическими носителями разума, сплошь и рядом — просто почти всегда неосознанно. 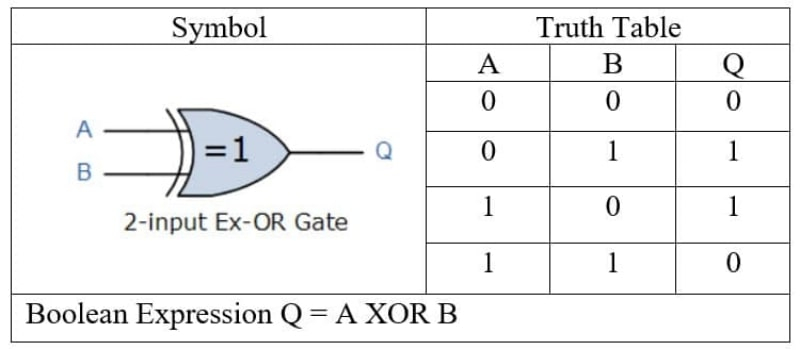
Обозначение вентиля «исключающее ИЛИ» в системе ANSI и таблица истинности для него в случае двух аргументов (источник: 911Electronic) «Исключающее ИЛИ» (XOR) для двух аргументов даёт на выходе «истину» только в том случае, когда значения этих аргументов разнятся, а вот если они совпадают, ответом будет «ложь»: XOR-функцию реализует, к примеру, любой регулярный поезд метрополитена, у которого с обоих концов прицеплены моторные вагоны кабинами наружу. Если ровно один из двух этих вагонов активен (размещённый в нём мотор работает), поезд движется в соответствующем направлении (значение на выходе — «истина»). Если оба мотора не действуют либо с равной мощностью пытаются тянуть состав каждый в свою сторону — поезд, разумеется, остаётся на месте (на выходе «ложь»). Критерий движения поезда метро можно записать в терминах математической логики так: мотор переднего вагона «исключающее ИЛИ» мотор заднего вагона. Розенблаттовский перцептрон при решении задачи в таком виде пойдёт, что называется, вразнос: раз за разом его будет сбивать с толку (нарушать уже вроде бы верно подобранное распределение весов) взаимное влияние вроде бы никак не связанных между собой исходных признаков. Значит, машине необходимо помочь — например, усложнив её конструкцию при помощи дополнительного перцептрона, который будет сопоставлять результаты анализа кажущихся независимыми входных параметров, верно? 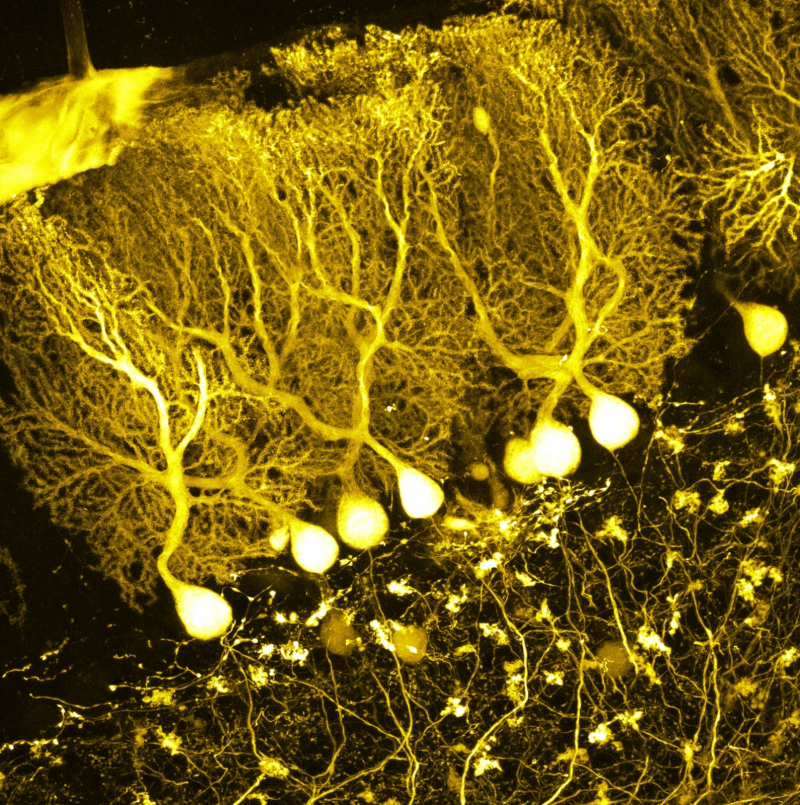
Для нейрофизиолога знание о том, что нейроны в мозге соединяются каскадами, тривиально — но инженерам на постижение этой истины потребовался немалый срок (источник: Wikimedia Commons) Сегодня это действительно может показаться само собой разумеющимся. Но на деле от изобретения одиночного перцептрона до формулировки идеи о возможности соединения их во взаимоувязанные комплексы прошло почти четверть века. Лишь в 1986 г. в работах Дэвида Румельхарта (David Rumelhart), Джеффри Хинтона (Geoffrey Hinton) и Рональда Уильямса (Ronald J. Williams) был изложен чрезвычайно перспективный метод расширения когнитивного потенциала перцептронных систем при помощи обратного распространения ошибки — backpropagation, или попросту BP. Принцип BP сводится к тому, что мало вместо одного искусственного нейрона взять несколько, которые отвечали бы за распознавание отдельных свойств изучаемых объектов (работает ли мотор в переднем или заднем вагоне), надо также вслед за первым слоем явного выявления признаков расположить по меньшей мере ещё один, скрытый, который отвечал бы за изучение связей между этими самыми признаками (работают ли оба мотора одновременно и с равной тягой). 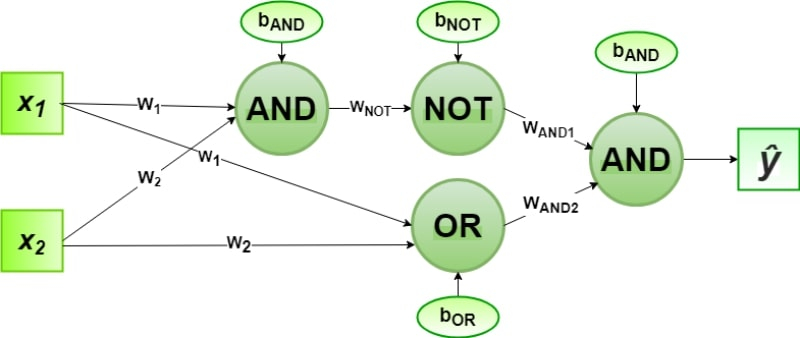
Многослойная перцептронная сеть уже позволяет реализовать логическую функцию XOR за счёт комбинации NAND (NOT и AND) с OR через AND при следующих значениях весов: w1=1, w2=1, wNOT=–1, wAND1=1, wAND2=1 — и нормировочных констант: bAND=–1,5, bOR=–0,5 и bNOT=0,5 (источник: GeeksForGeeks) И действительно, с использованием второго слоя перцептронов реализовать функцию XOR оказывается не так уж сложно. Она сводится к комбинации «логического ИЛИ» (OR) и «логического И-НЕ» (NAND) через «логическое И» (AND). Каждая же из трёх этих функций, в свою очередь, без труда реализуется одиночными перцептронами. 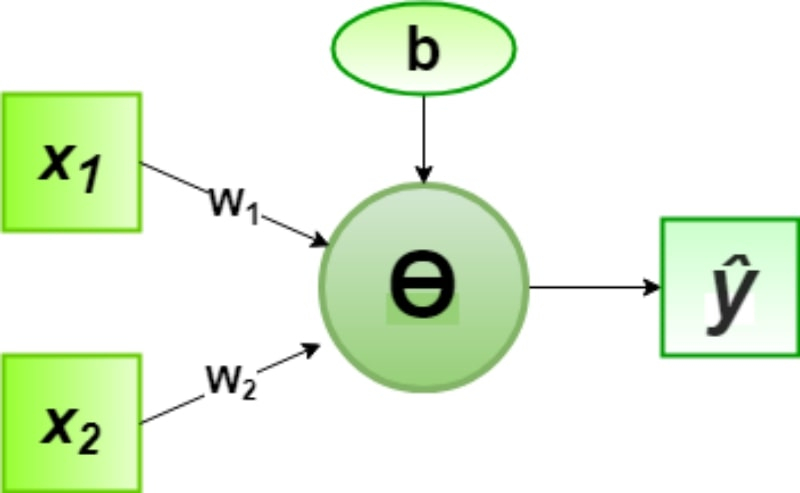
Одиночный перцептрон с порогом активации Ө (если взвешенная сумма аргументов ≥0, на выходе 1, иначе 0) позволяет реализовывать базовые логические функции: какие именно — AND, OR, NOT и так далее — определяют значения константы b и весов w1 и w2 (источник: GeeksForGeeks) Чтобы не перегружать изложение основных принципов нейронных сетей прикладной математической логикой, приведём самый простой вариант — воплощение «логического И» на розенблаттовском перцептроне. Здесь имеются три входа: нормировочная константа b (от англ. bias — «смещение»), в данном случае имеющая значение –1, и переменные x1 и x2, которые могут принимать значения 1 или 0. Таблица истинности для «логического И» наверняка многим знакома:
Перцептрон, напомним, взвешенно суммирует все поступающие на его входы сигналы и, если результат выходит положительным, выдаёт единицу по выходному каналу, и ноль — если сумма меньше или равна нулю. Веса в данном случае равны +1 для обоих аргументов (w1 и w2); сами же эти аргументы (x1 и x2) принимают значение 1 или 0. Соответственно, работа перцептрона для каждой строки таблицы истинности будет выглядеть так:
По тому же принципу, но с использованием других наборов весов перцептроны превращаются в логические вентили OR, NOT, NOR или NAND, и только для XOR и XNOR требуется добавление второго слоя с соответствующими весами, который будет компенсировать ошибки, возникающие из-за невозможности учёта более сложных взаимосвязей отдельных параметров и элементов изучаемой машиной модели. ⇡#Сколько вешать в граммах?Для получения базовых логических вентилей перцептроны несложно настроить вручную, подбирая веса буквально на глаз. К примеру, если по только что описанной схеме попытаться воплотить «логическое ИЛИ-НЕ» (NOR) с прежней нормировочной константой b = –1, получится неверный ответ уже в самой первой строчке таблицы истинности. Ведь результатом 0 NOR 0 должна быть единица, а у нас: –1 +0 * w1 + 0 * w2 = –1, то есть на выходе перцептрона окажется 0. Значит, надо поменять b на +1, а дальше подбирать подходящие синаптические веса w1 и w2, тщательно сверяясь с таблицей истинности, — они окажутся равными –1 каждый.
Наглядный принцип работы многослойной сети перцептронов, идентифицирующей объект по сепарабельному (подразумевающему чёткую дихотомию, ответ «да — нет») признаку: кошка или собака? (источник: Techaroha) Очевидно, однако, что ручной подход срабатывает лишь для простейших схем, реализующих базовые операции математической логики. У перцептрона могут быть десятки и сотни входов (у биологического нейрона их, напомним, могут насчитываться тысячи), и машина сама должна корректировать синаптические веса на каждом из них, отталкиваясь только лишь от того, подтверждает оператор результат очередной попытки распознать нужный образ на выходе (либо решить иную стоящую перед нейросистемой задачу) — или нет. Как же всё это осуществляется на практике? Для этого, собственно, и придуманы многослойные перцептроны (multi-layer perceptron, MLP), действующие по принципу обратного распространения ошибок. Простейшие их разновидности — уже упомянутые чуть выше двуслойные мини-нейросети для реализации логических операторов XOR и XNOR. Самообучающиеся же (точнее, обладающие возможностью эффективной самокоррекции синаптических весов) MLP состоят из множества слоёв со значительным числом искусственных нейронов в каждом, причём выходы перцептронов предшествующего слоя (функциональные аналоги отростков на аксоне биологического нейрона) служат входами для перцептронов последующего. Собственно, когда специалисты по нейрокомпьютингу говорят о глубоком обучении, это не красивая метафора, а вполне прагматичное указание на то, что число скрытых слоёв в нейросети превышает два. 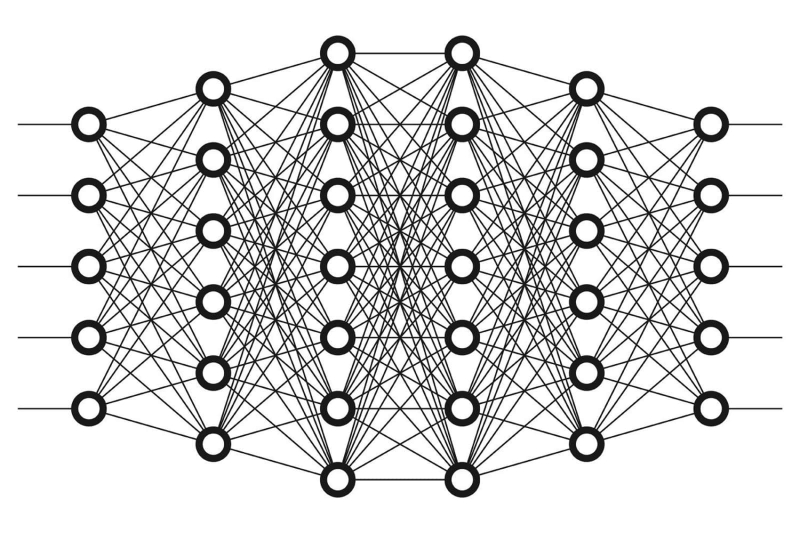
«Глубокое обучение» подразумевает использование многослойной нейронной сети (источник: Wikimedia Commons) Вообще говоря, такая сеть уже представляет собой достойную модель коры головного мозга — по крайней мере для реализации целого ряда специализированных задач она прекрасно годится. Исходно, разумеется, MLP чист — в том смысле, что синаптические веса на входах его элементарных перцептронов в каждом слое случайны, и потому система в целом не способна к каким бы то ни было результативным действиям. Однако в ходе обучения с учителем (supervised learning) системе демонстрируются длинные ряды объектов, помеченные как принадлежащие определённым классам. В результате такого обучения система начинает с весьма высокой точностью классифицировать ранее не встречавшиеся ей объекты уже полностью самостоятельно. Смысл термина «обратное распространение ошибок» в применении к самообучающейся нейросистеме заключается в том, как именно она корректирует допущенные в ходе распознавания образов неточности. Само понятие «распознавание образов» здесь используется максимально широко: MLP может воспринимать или синтезировать человеческую речь, создавать графическое изображение на основе текстового описания или идентифицировать определённое лицо в многотысячной толпе на видеокадре. 
Изображение, сгенерированное нейросетью Imagen с использованием в качестве ввода фразы «Three spheres made of glass falling into ocean. Water is splashing. Sun is setting» (источник: Google) Во всех этих и подобных случаях нейросистема производит сопоставление некоего конкретного объекта и обобщающей идеальной группы («класса»). Изображённое на данном снимке животное может относиться или не относиться к классу «собака»; воспроизведённая электросинтезатором фонема может относиться или не относиться к классу «естественная человеческая речь» и так далее. Оценку «да или нет», «относится или не относится» в процессе обучения под наблюдением выставляет биологический оператор, а система — если оценка эта не положительная — снова и снова меняет синаптические веса в одном слое за другим, начиная с самого дальнего от входа, чтобы добиться наконец подтверждения. Процедуру эту можно представить следующей схемой: a) синаптические веса во всех слоях задаются случайными малыми по модулю числами, b) MLP инициируется набором входных данных, который затем проходит через все слои, и на выходе формируется некий результат, c) наблюдатель оценивает результат и возвращает его машине; на основе сравнения полученного результата с желаемым определяются градиенты функции потерь для каждого из весов, d) векторы этих градиентов указывают на направление роста функции потерь; соответственно, в противоположном направлении та убывает — и веса корректируются таким образом, чтобы на следующей итерации функция потерь, предположительно, стала меньше, e) MLP снова инициируется прежним набором входных данных, и, если отличие результата от идеала меньше, чем в прошлый раз, синаптические веса вновь корректируются в прежнем направлении, в противном же случае градиенты функции потерь вычисляются заново, f) и так до тех пор, пока отличие выдаваемого нейросетью результата от идеала станет, на взгляд обучающего, меньше некой заведомо приемлемой величины. ⇡#Если долго вглядываться в тройкуПриведём пример довольно детального, но несложного по сути объяснения принципов глубокого обучения, предложенный экспертами Института инженеров в области электротехники и электроники (Institute of Electrical and Electronics Engineers, IEEE). Здесь условно изображена многослойная нейронная сеть, обучающаяся распознавать рукописную цифру «3»: 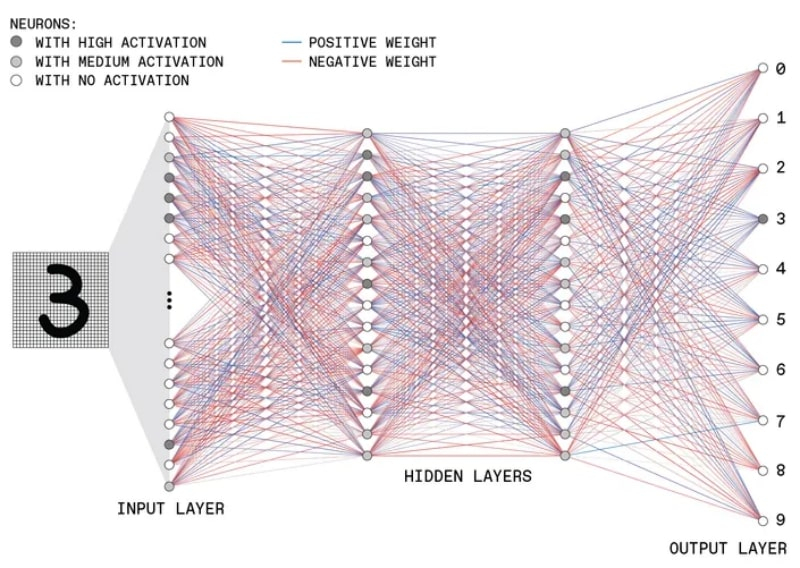
Общая схема MLP с двумя скрытыми слоями, распознающего рукописные цифры. Оттенок серого в кружках указывает на величину выходного сигнала каждого перцептрона по модулю, цвет линии (синий или красный) — на его знак: с плюсом он соответственно будет учитываться или с минусом (источник: IEEE) На вход MLP поступает разбитое на пикселы изображение, и каждый пиксел обрабатывается отдельным перцептроном первого слоя. Затем выходные сигналы с этих перцептронов передаются в глубину. Перцептроны же последнего слоя выдают «солидарное решение» всей системы в целом: что за рукописная цифра была на входе. Ответом в данном случае должно стать «3», и вот как к этому приходит глубокая нейронная сеть: 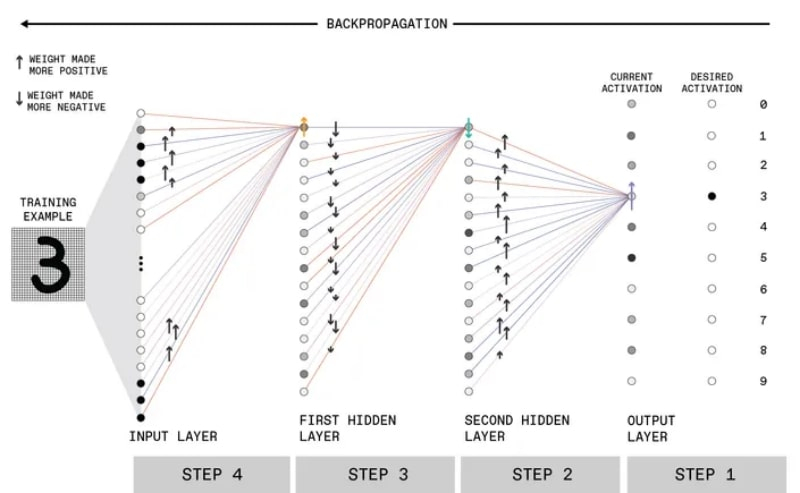
Та же схема, но с акцентом на том, какими сигналами из предыдущего слоя активируется лишь один перцептрон в последующем и как на основании анализа этих сигналов производится обратное распространение ошибки (источник: IEEE) На первом шаге (он крайний справа, поскольку отталкиваться надо от соответствия сделанного сетью вывода ожидаемому ответу) случайные веса, которыми были исходно инициированы синаптические связи, привели к немного предсказуемому результату: нейронная сеть решила, что на картинке цифра «5» (самый тёмный серый кружок в колонке current activation). В ответ экспериментатор сообщает MLP об ошибке, повышая веса синаптических связей, ведущих к значению «3», на ближнем к нему слое перцептронов. Здесь важно обратить внимание на различия в оттенках серого: искусственные нейроны действуют по несколько иному принципу, чем биологические. Если сумма пришедших от синаптических связей входных сигналов (с учётом весов) меньше заданного порогового значения, на выходе перцептрона сигнала нет, — это полностью соответствует поведению нейрона в мозге. Однако после преодоления порога активации живой нейрон порождает электрические импульсы (стробы) примерно равной амплитуды — хотя порой и плотными группами, если уровень стимуляции велик. Перцептрон же, если выполнено условие его срабатывания, выдаёт сигнал, по величине равный той самой взвешенной сумме входных сигналов, — выступает фактически как селективный суммирующий передатчик. Как раз поэтому величина выходного сигнала от перцептрона в текущем слое даёт чёткое представление о влиянии на него искусственных нейронов из предыдущего слоя — что и создаёт основу для тонкой настройки нейронной сети на решение данной конкретной задачи. Второй шаг представляет собой то самое обратное распространение ошибки (точнее было бы сказать «сигнала об ошибке»), что подразумевается термином backpropagation. Синаптические связи, ведущие от перцептронов предпоследнего слоя к тому, что отвечает за формирование ответа «3» в последнем, получают команду на коррекцию весов в сторону увеличения. При этом чем выше было исходное значение каждого данного веса (чем темнее обозначающий перцептрон кружок на схеме), тем сильнее в определённой пропорции увеличивается вес связи с ним (это обозначает длина стрелочки на соответствующей линии). По какой конкретно формуле производится этот расчёт — для целей общего понимания несущественно. Важно, что это именно формула (та самая функция потерь, о которой упоминалось чуть ранее), прекрасно поддающаяся программированию, — и потому ручное воздействие биологического оператора на систему на этом этапе, как и на всех последующих, не требуется. Строго говоря, если обучающие карточки исходно размечены (наряду с рукописной тройкой MLP получает машиночитаемое сообщение «3», с которым результат распознавания сопоставляется в финале), то нейронная сеть и вовсе не будет нуждаться в операторе для обучения — по крайней мере для задач подобного класса. На третьем шаге показано, каким образом понижается значимость для формирования итогового ответа тех перцептронов, вклад которых в формирование решения «3» отрицателен. Для примера взят верхний перцептрон во втором скрытом слое: допустим, его влияние необходимо уменьшить (зелёная стрелка вниз). Для этого применяется та же процедура, что и на предшествующем шаге, но с обратным знаком: чем выше вклад очередного перцептрона из первого скрытого слоя в активацию данного искусственного нейрона, тем сильнее (по модулю) будет корректирующее воздействие. Точно таким же образом производится коррекция весов для синаптических связей искусственных нейронов первого скрытого слоя с внешними перцептронами, напрямую воспринимающими разбитую на пикселы тренировочную картинку. ⇡#Тонкости восприятияМожет показаться, будто развитие нейронных сетей происходило линейно и поступательно. Отнюдь: ещё в 1969-м Марвин Минский (Marvin Minsky) и Сеймур Пейперт (Seymour Papert) опубликовали книгу «Перцептроны: введение в вычислительную геометрию», в которой резко раскритиковали ограниченность области применения розенблаттовских искусственных нейронов — приведя, в частности, рассмотренный нами пример с «исключающим ИЛИ». Только к началу 1980-х фоннеймановская вычислительная техника развилась настолько, что позволила моделировать сложные логические структуры (включая многослойные нейронные сети с обратным распространением ошибок), — это и привело к новому расцвету нейрокомпьютерного направления. 
В ходе обучения Watson Health с учителем использовалась экспертиза множества медицинских специалистов (источник: IBM) Тем не менее даже сегодня этому направлению есть ещё, мягко говоря, куда развиваться — невзирая на все объективные успехи, достигнутые разработчиками нейросетей. Достаточно упомянуть проект Watson Health, в который IBM годами инвестировала миллиарды долларов. Этот проект ставил своей целью революционизировать медицинскую науку, избавив учёных от необходимости лично перелопачивать десятки и сотни статей с релевантными исследованиями, чтобы отыскать в них действительно ценную и важную информацию для лечения конкретных пациентов. Задача казалась простой — тем более что после победы суперкомпьютера Watson в американской телевикторине Jeopardy (эта франшиза у нас известна как «Кто хочет стать миллионером?») ещё в 2011 году стало очевидно, насколько хорошо машина способна отвечать на вопросы, ответы на которые ранее уже были найдены и зафиксированы в текстовом виде. Команде разработчиков Watson (10 стоек по 10 серверов IBM Power 750 плюс десятки тысяч строк кода, формирующего виртуальную многослойную нейросеть) явилась светлая идея: что, если приложить эту поисковую мощь к огромному объёму уже опубликованных и продолжающих копиться каждый месяц научных статей по медицинской тематике? 
Стоечные серверы Power 750, ставшие аппаратной основой для программной нейросети Watson Health (источник: IBM) Проект Watson Health, стартовавший в 2015 г., был нацелен на то, чтобы выискивать в научных работах и сопоставлять между собой симптомы заболеваний, с одной стороны, и рекомендации по их излечению, с другой. В идеале это позволило бы ставить корректный диагноз онлайн: лечащему врачу (даже без узкоспециального образования) достаточно было бы переправить системе зафиксированные им у пациента симптомы, а также результаты анализов и иных специальных исследований. Нейросеть же определяла бы автоматически по этому набору вводных болезнь — и подыскивала для неё наилучшие на данный момент лекарство (включая только что вышедшие и даже экспериментальные) и методику лечения. И всё это — на основе обширной базы медицинских журналов, пополняющейся на тысячи только англоязычных статей каждый месяц. Однако ничего не вышло, и в начале 2022 года IBM решила продать Watson Health частной акционерной компании Francisco Partners. Выяснилось, что перелопатить сотни тысяч статей нейросеть действительно способна без особого труда. Но, в отличие от игры Jeopardy, медицинские вопросы далеко не всегда имеют заведомо точные ответы. Одно и то же явление разные учёные и разные научные школы могут трактовать по-своему. Немало (увы, даже удручающе много) статей оказались основаны на неполных, дурно верифицированных или попросту подложных данных. 
Изображение, сгенерированное нейросетью Imagen с использованием в качестве ввода фразы «A strawberry mug filled with white sesame seeds. The mug is floating in a dark chocolate sea» (источник: Google) Сведущий биологический эксперт в некой конкретной области знаний способен если не распознать с ходу негодную статью, то по меньшей мере усомниться — на основании накопленных знаний и опыта — в обоснованности сделанных автором выводов. Нейросеть — так не умеет, и потому пользы от практического применения Watson Health оказалось по сути не больше, чем от постановки медицинского диагноза неспециалистом, просмотревшим пару сезонов «Доктора Хауса» и умеющим формулировать запросы к популярной поисковой машине. И даже если задаться целью подавать на вход нейросети исключительно корректно организованные, верифицированные маститыми экспертами научные труды, гарантией идеальной работы машинного «разума» это не станет. Дело в том, что глубокие (многослойные) перцептронные нейросети принципиально уязвимы к ошибкам качества приближения (goodness of fit), причём двух видов сразу: недоадаптации и переадаптации (underfitting и overfitting соответственно). ⇡#Что такое недоадаптация и переадаптацияНейросеть самоорганизуется, подстраивая веса на синаптических входах перцептронов в своих слоях, с целью наилучшим образом распознавать обучающий набор данных, а затем — с этим же самым комплектом весов — пытается классифицировать совершенно новые для себя данные. Недоадаптация и переадаптация — две крайности, в которые при этом, увы, чрезвычайно просто свалиться. 
Недоадаптация: модель слишком проста, чтобы адекватно учесть характер распределения данных (источник: University of New South Wales) Недоадаптация возникает, если построенная нейросетью модель (комплект синаптических весов в каждом слое) чрезмерно проста. Простая модель чаще всего описывает почти всё что угодно — но со значительным отклонением предсказания от наблюдения в каждой конкретной точке. Едва ли не любой набор экспериментальных точек можно в первом приближении аппроксимировать прямой линией, но ценность предсказаний, сделанных на основе такой тривиальной модели, вряд ли окажется велика: 
Переадаптация: модель воспроизводит каждую точку в наборе экспериментальных данных (источник: University of New South Wales) Переадаптация, напротив, обусловлена избыточной фиксацией модели на деталях. В результате тестовый объект будет распознаваться нейросетью идеально, однако стоит его немного изменить — например, повернуть картинку буквально на пару градусов, — и система уже не сможет его «узнать». 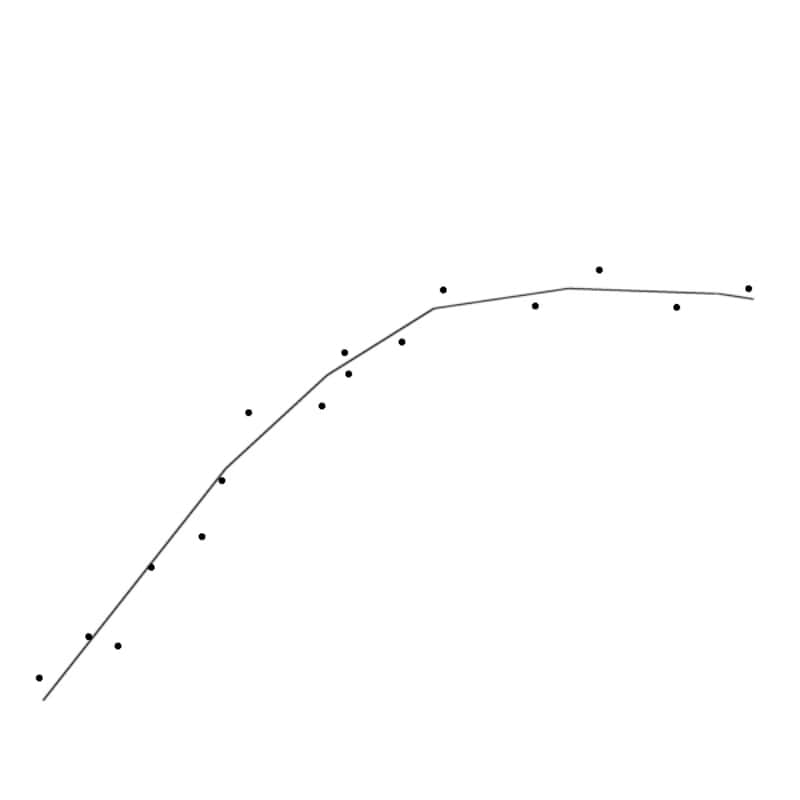
Корректно обученная MLP оптимальным образом аппроксимирует проведённые эксперименты и позволяет адекватно предсказывать результаты будущих (источник: University of New South Wales) Разработчики нейронных сетей стремятся оптимизировать как их устройство, так и процесс обучения — с тем, чтобы не допускать недо- или переадаптацию. В идеале модель объекта, образованная сочетанием конструкции MLP с комплектом синаптических весов, должна адекватно учитывать неизбежную дисперсию реальных измерений. И хотя на этом направлении развития нейронных сетей очевиден немалый прогресс, тёмным пятном на их репутации продолжает оставаться непостижимый для человеческого разума принцип принятия ими тех или иных решений. Да, точные значения синаптических весов для каждого перцептрона в каждом слое обученной нейросети тренирующим её программистам известны. Но внятно объяснимого смысла они не имеют — и потому работа MLP продолжает оставаться «чёрным ящиком», что во многих случаях попросту недопустимо. Одно дело, когда не очень ясно, по каким именно критериям машина безошибочно классифицирует фото кошечек и собачек: справляется — и хорошо. Совсем другое — когда она определяет, что делать автономному автомобилю, на перекрёсток перед которым под красный для себя свет внезапно выскочил велосипедист: тут уже хочется гораздо большей определённости в мотивациях — страховой компании и возможному следствию они бы крайне пригодились. Именно поэтому так активно в последние годы развивается направление объяснимых нейронных сетей, логику принимаемых которыми решений можно явно контролировать. И более того — появляется возможность отвергать заведомо неприемлемые решения, если они противоречат неким исходным принципам. Тут уже и до практической реализации азимовских законов робототехники, кажется, недалеко, однако пока работы для программистов и инженеров остаётся непочатый край. 
Искусственные нейроны вроде этого прототипа на основе допускающих смену фазового состояния материалов, созданного IBM в 2016 г., могут стать основой для ещё более эффективных нейронных сетей (источник: IBM) Моделирование нейросетей в памяти фоннеймановских машин — удовольствие по множеству параметров затратное. Практичнее было бы реализовывать их на аппаратной основе, более близкой по энергоэффективности к биологической нервной ткани. Но это всё же дело отдалённого будущего, а пока что и на полупроводниковой элементной базе нейронные сети играют на бирже эффективнее среднего брокера, лучше умелого повара готовят картошку фри и луковые колечки и даже создают картинки и видеоклипы, отталкиваясь от текстовых описаний (например, «плюшевый медведь моет посуду»). То ли ещё будет!
⇣ Содержание
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
|