Полная гомоморфность — и никакого доверия! / Искусственный интеллект

Выход есть — применять полностью гомоморфное шифрование, что позволяет производить операции над данными, не переводя их из закодированного состояния в открытое. Результат таких операций также выходит зашифрованным, причём по тому же алгоритму и с тем же ключом, что и исходные данные. Владелец их может таким образом получить в своё распоряжение нужную ему информацию, добытую в облаке облачными же вычислительными средствами, — избавляя тем самым себя от затрат на содержание локальной ИТ-инфраструктуры и не поступаясь конфиденциальностью ни итоговой информации, ни исходных данных. Подход здравый и крайне полезный для множества самых разнообразных приложений, от медицинских до электоральных, — правда, для эффективного гомоморфного шифрования лучше всего подходят специализированные вычислители, несколько отличные от повсеместно распространённых процессоров общего назначения.

Один из разворотов известного манускрипта Войнича, который также именуют иногда «Священным Граалем криптографии»: занятно, что он, даром что изучен в прикладном плане буквально от корки до корки (точно известно количество слов в нём, частота встречаемости отдельных символов, даже толщина и примерный год выделки каждой из пергаментных страниц), так и не расшифрован, — вполне в духе гомоморфного подхода (источник: Wikimedia Commons)

⇡#Так, да не так

Гомоморфизм в математике определяется для пары алгебраических систем (которые, в свою очередь, могут быть группами, кольцами или полями) как отображение операций над элементами одной их этих систем в другую. Допустим, есть группа G, для элементов которой определена операция x ○ y (какая именно операция — пока что значения не имеет; скажем, банальное сложение), и группа F со своей, отличной от той операцией над уже её элементами — a ● b (а вот тут уже операция может быть совершенно иной — для примера, взятие логарифма от первого операнда по основанию, заданному вторым). Так вот, гомоморфизмом групп f (записывается как f:G→F) называется такое отображение G в F, при котором для любых принадлежащих G элементов x и y выполнено равенство

f(x ○ y) = f(x) · f(y)

То бишь некоторому действию с элементами первой группы будет соответствовать (не обязательно взаимно однозначно, кстати, — обязательное требование обратимости тут отсутствует) уже другая, определённая для второй группы операция над образами элементов первой. Собственно, само существование алгебраических систем, допускающих гомоморфизм, и гарантирует возможность оперировать отдельными элементами зашифрованных данных, не обладая доступом к ключу шифрования. Бесспорно, обращаться таким образом можно далеко не со всякими шифрами: известны схемы кодирования данных с разными уровнями гомоморфности — т. е. с поддержкой различных операций. И полностью гомоморфным — fully homomorphic encryption (FHE) — называют шифрование по такой схеме, что позволяет производить вычисления на разных уровнях глубины (имеется в виду число последовательных операций над каждым элементом в ходе таких вычислений), да ещё и проводя операции различных типов. Неудивительно, что FHE нередко называют «Священным Граалем» криптографии: оно позволяет производить операции, включая достаточно сложные, над элементами зашифрованных данных на заведомо недоверенных компьютерных системах — в том же публичном облаке, — вовсе не используя в ходе вычислений секретный криптографический ключ, с которым эти данные исходно были закодированы.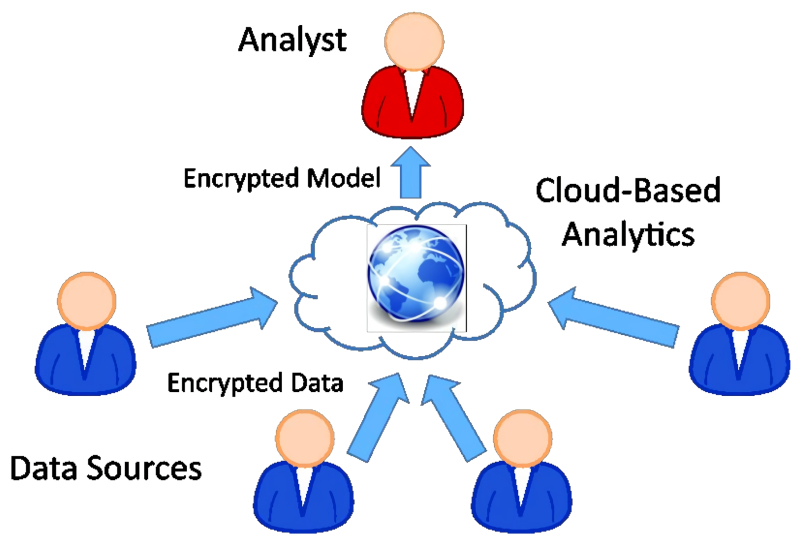

Пример практического применения FHE: провайдеры медицинских либо иных чувствительных данных загружают те в облако в зашифрованном виде, а аналитик, располагая гомоморфным инструментарием для обработки этих данных, получает на их основе — зашифрованную же! — обобщающую информацию (в примере с медицинскими данными это может быть определение вероятности проявления больничных инфекций в разных медучреждениях, скажем). При этом ни провайдеры исходных данных не имеют прямого доступа к результатам их обработки, ни аналитик — к «сырым» данным, ни владелец облака — ко всему, что происходит на предоставленных им в аренду серверах и СХД (источник: Wikimedia Commons)

Хотя идея гомоморфного шифрования буквально носилась в воздухе с тех самых пор, как возникла и принялась развиваться компьютерная криптография (именно компьютерная, позволяющая благодаря применению машин проводить весьма сложные вычисления за ограниченное время), обретать практические контуры она начала лишь в 1970-х, тогда ещё под именем «конфиденциального гомоморфизма» (privacy homomorphism). Многие исследователи и практики криптографы предлагали развивать такие схемы шифрования, которые будут позволять выполнение хотя бы простейших операций — сложения и умножения — над зашифрованными операндами без их раскодирования. Появившийся в 1977 г. алгоритм RSA, во многом определивший дальнейшие пути развития цифровой криптографии, изначально оказался гомоморфным в смысле умножения (multiplicatively homomorphic), поскольку основная его операция — это возведение в степень:

C = (m^x) · (mod n)

где C — получаемый в ходе шифрования текст, m — исходный (кодируемый) текст, x — секретный ключ, а n — произведение двух простых чисел. Операция mod (сокращение от «modulo», по-русски — «взятие остатка от деления по указанному модулю»), подразумевает, что стоящее слева от mod число делится на то, что справа (собственно n), и результатом её оказывается ноль — если первое число нацело делится на второе, — либо какое-то целое число меньше делителя, если не делится, т. е. 9 mod 3 = 0, 9 mod 2 = 1. Строго говоря, вычислительная операция mod не тождественна прямолинейной процедуре взятия остатка, если речь идёт об отрицательных числах, но в данном случае это не принципиально. Важно иное: согласно правилам возведения в степень,

aⁿ · bⁿ = (ab)ⁿ

Иными словами, перемножение двух шифротекстов, закодированных с одним и тем же ключом, эквивалентно — именно в случае базового алгоритма RSA — возведению произведения обоих исходных текстов этих шифротекстов в степень, заданную тем самым ключом; именно по этой причине можно умножать закодированные в RSA числа и получать на выходе осмысленный результат. Очевидно, этот алгоритм не претендует на реализацию концепции FHE — он не полностью гомоморфен, — но сам термин «гомоморфное шифрование» был, судя по всему, впервые введён в широкий оборот именно Рональдом Ривестом (Ronald L. Rivest), Леонардом Адлеманом (Len Adleman) и Майклом Дертузосом (Michael L. Dertouzos), разработчиками оригинального RSA, в работе «О хранилищах данных и конфиденциальных гомоморфизмах», изданной в 1978 г. Именно эти исследователи предложили отыскивать такие операции над числами, которые позволили бы реализовывать полностью гомоморфное шифрование, — как раз из соображений предельной надёжности хранения данных и извлечения информации из них в недоверенных средах.

Сводка основных методов FHE, порождённых работой Джентри, всего за первый неполный десяток лет после её публикации. Обратим внимание, что на идеальных решётках основан один только оригинальный алгоритм, — последователи, оценив красоту и изящество предложенной идеи, для практических приложений отыскивали всё же более эффективные в вычислительном плане, пусть порой и несовершенные в других отношениях, схемы (источник: IEEE)

Однако путь к FHE, реализованному на уровне алгоритма (чуть позже станет понятно, почему здесь подчёркивается именно математическая достижимость такого шифрования — в отрыве от прикладной его реализации), занял почти четыре десятка лет. Сперва исследователи нашли способ кодировать данные лишь с кое-какой, или, если благозвучнее, частичной гомоморфностью (somewhat homomorphic encryption, SHE, — это не ироничная характеристика промежуточного метода, а вполне солидное его наименование); когда, допустим, на глубину в пять операций сложения/умножения гомоморфизм сохраняется, а шестая уже порождает недекодируемый с исходным ключом, т. е. бессмысленный с точки зрения оператора, результат. В процессе работы над SHE исследователи обнаружили, что алгоритмическая сложность предлагаемых ими схем кратно возрастает, если требуется комбинировать пусть даже конечное число операций умножения и сложения, — это на время заставило многих усомниться в принципиальной достижимости «Священного Грааля» FHE на практике. В том смысле, что формальный математический запрет на построение такого алгоритма отсутствует, верно, — вот только после обнаружения подходящей схемы может оказаться, что для имеющейся в наличии вычислительной техники реализация её запредельно ресурсоёмка.

⇡#Торжество логики

В 2009 г. американский кибернетик Крейг Джентри (Craig Gentry), который в то время был аспирантом Стэнфордского университета и стажировался в IBM, опубликовал диссертацию на соискание степени доктора философии — «Алгоритм полностью гомоморфного шифрования». Именно она стала отправной точкой для всех последующих схем FHE, в которых применяются сложение и умножение операндов на произвольную глубину. Предложенная Джентри оригинальная криптосистема достаточно сложна — она оперирует идеальными n-мерными целочисленными решётками. К тому же в процессе кодирования система формирует особый шумовой вектор, с использованием которого исходный текст сообщения преобразуется в шифротекест. Это существенно повышает криптостойкость схемы Джентри, поскольку практически сводит на нет любые проявления изначальной упорядоченности текста (вроде частоты встречаемости символов естественного языка), но приводит к накоплению ошибок — так, что после определённого количества вычислений раскодировать сообщение становится невозможно. Здесь, кстати, стоит отметить, что раз речь идёт о компьютерном приложении предложенной схемы, то числа, над которыми производятся операции, — двоичные. А это, в свою очередь, означает исчерпывающую полноту FHE, поскольку для логических «0» и «1» по сути все операции сводятся к сложению и умножению, то бишь к логическим «НЕ», «И» и «ИЛИ».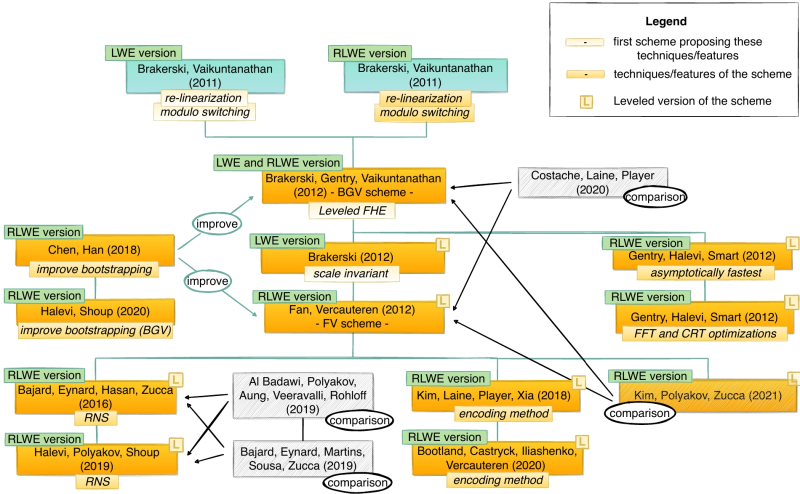

Генеалогическое древо второго поколения схем FHE начало развиваться с 2011 г. по двум направлениям — через решение вычислительных задач LWE (Learning With Errors) и RLWE (Ring Learning With Errors) (источник: IEEE)

FHE недаром называют не только «Священным Граалем», но и «швейцарским армейским ножом» современной криптографии: это поистине универсальный подход к операциям над закодированными данными. Суть в следующем: прикладная криптография не сводится к операции «кодирование — передача/хранение — расшифровка», как это сплошь и рядом показывают в шпионских фильмах. Да, обмен шифрованными данными важен для рыцарей плаща и кинжала, но на практике существует куда больше задач, при решении которых важны не сами данные, а некие операции над ними. Многоагентная обработка информации (когда один агент поставляет сырые данные, другой — алгоритмы для извлечения из них статистических закономерностей, третий — аппаратную основу и линии связи, и никто из них не должен иметь прямого доступа к тому, что делает/знает другой), электронное голосование (да-да, в отсутствие FHE эта система вырождается в банальную игру общества в «верю/не верю» с назначенным государством оператором расшифрованных данных), протокол доказательства с нулевым разглашением (zero-knowledge proof), когда проверяющая сторона удостоверяется в корректности утверждения стороны доказывающей, не раскрывая самого этого утверждения, — всё это изящно и просто реализуется в подходе FHE. Притом, отметим, для каждой из перечисленных и многих иных криптографических задач выработаны специализированные средства реализации, однако только в рамках FHE возможно исполнение их всех разом, на общей платформе, без привлечения дополнительных схем кодирования и аппаратных средств. И это — огромное достоинство полностью гомоморфного шифрования, даже с учётом не самой скромной его ресурсоёмкости.

Строго говоря, предложенная Джентри схема представляла собой не прикладной рецепт, а, скорее доказательство самой возможности алгоритмической реализации FHE: исследователь рассмотрел построение схем SHE, к тому времени уже неплохо освоенных, в том числе и на практике, и продемонстрировал, что если такая схема будет обеспечивать верификацию своего же собственного алгоритма дешифровки (добавив к тому ещё несколько дополнительных условий), то SHE естественным образом трансформируется в FHE. Тонкость предложенного подхода — и огромное достижение Джентри, который нашёл из этой криптографической теснины красивый выход, — в том, что указанная процедура верификации требует изрядного количества вычислений, а участие в них шумового вектора ведёт к неизбежному накоплению ошибок. Совершенно естественный путь для устранения такого рода — с точки зрения чистой математики — прямолинеен и прост: не доходя до опасной черты, остановить гомоморфные операции, декодировать промежуточные результаты, после чего снова их зашифровать — и продолжить вновь, пока вычислительная ошибка опять не приблизится к критическому уровню.

Реализация бутстрэппинга в FHE — сравнительно простая и глубоко логичная процедура (источник: IEEE)

Но вот беда: требование расшифровки промежуточных результатов на корню убивает практический смысл FHE. Придётся ведь выгружать данные из условно недоверенной среды, производить над ними операции, закачивать обратно, — и при этом возникает опасность нарушения конфиденциальности сторонних операторов. Как в случае организации биржевой торговли зерном, например: трейдеры хотели бы принимать в расчёт данные не только о спросе, но и о предложении — какова динамика поступлений нового зерна на склады фермеров, сколько фактически они могут отгрузить по заявкам прямо сейчас и т. д. Фермеры, в свою очередь, вовсе не заинтересованы в том, чтобы посвящать биржевиков в свои проблемы — неурожай у них, переполненные элеваторы, нашествие мухи-горбатки или ещё какие напасти, — из опасения, что непосредственную выгоду из этого извлекут именно трейдеры. Формула для определения «честной» биржевой цены в зависимости от уровней спроса и предложения достаточно проста, но если обе стороны (конечных покупателей зерна пока оставим за скобками — им тратить деньги в любом случае) видят, чтó за переменные подставляют в неё их контрагенты, трейдер как занимающий более выгодную позицию посредника в финансовом потоке оказывается в заведомо выигрышном положении: он может скорректировать свои данные на лету. И потому здесь разумно использовать FHE, чтобы на выходе действительно получалась справедливая цена: формула применяется к зашифрованным данным, загруженным, с одной стороны, фермерами (о предложении), с другой — биржевиками (о спросе). Само собой, трейдеры всегда будут стремиться получить ценную информацию по косвенным признакам, но однозначной картины те — в отличие от предоставленных самими фермерами данных о фактической готовности зерна к отгрузке — не дают. Понятно, что, если на некотором этапе таких чувствительных вычислений промежуточный результат придётся куда-то выгружать для последующей расшифровки с профилактическим перекодированием, вероятность утечки данных возрастёт многократно.

Основная идея Джентри как раз и заключалась в том, чтобы подобрать такие SHE, которые могли бы верифицировать свои собственные алгоритмы гомоморфно. Такой рекурсивный в некотором смысле подход (полная гомоморфия реализуется через гомоморфию же, но промежуточных шагов) в вычислительной математике называют бутстрэппингом, от английского bootstrap — названия той петельки на заднике или боковой стороне ботинка, потянув за которую можно с лёгкостью надеть обувь без помощи рожка. Фраза «to pull yourself up by your bootstraps» в значении «вытянуть себя [из безвыходной ситуации] за петельки на ботинках» фиксируется в американском политическом дискурсе с первой трети XIX века и по смыслу соответствует куда более известной в наших краях истории о славном на весь свет своей честностью бароне — тот как-то вытянул себя за косичку парика из болота вместе с конём.

Суть бутстрэппинга, или самовытягивания, в приложении к частично гомоморфной схеме кодирования заключена в том, что берётся уже существенно зашумлённый шифротекст, берётся зашифрованный секретный ключ (да, он зашифрован публичным ключом, и в общем случае это небезопасно, но Джентри указал, каким образом сделать это, не компрометируя секретный ключ) — и производится гомоморфное раскодирование первого вторым. Производится, напомним, всё там же, в пределах недоверенной вычислительной среды. На выходе, если корректно подобрать схему реализации SHE (такие схемы называют «самовытягиваемыми» — bootstrappable), получится очередное зашифрованное представление исходного текста — но уже либо незашумлённое вовсе, либо только со следовыми остатками шума. Очень грубо говоря, происходит это из-за того, что в ходе гомоморфного преобразования уровни шумов перемножаются между собой, и, поскольку у только что зашифрованного секретного ключа этот уровень практически нулевой, произведение его на конечный уровень шума шифротекста также даёт по сути ноль. Взятие же в качестве второго сомножителя именно секретного ключа (который, напомним, применяли, чтобы закодировать шифротекст), а не условной единицы или какого-то произвольного числа позволяет не добавлять в закодированное сообщение лишних сущностей. Более детальное описание этого подхода можно отыскать в работе Computing Blindfolded: New Developments in Fully Homomorphic Encryption Винода Вайкунтанатхана (Vinod Vaikuntanathan), вместе с которым (и ещё с Цвикой Бракерски, Zvika Brakerski) Крэйг Джентри был удостоен в 2022 г. престижнейшей в кибернетических кругах премии Гёделя — кстати, за работу о полностью гомоморфном шифровании уже без бутстрэппинга.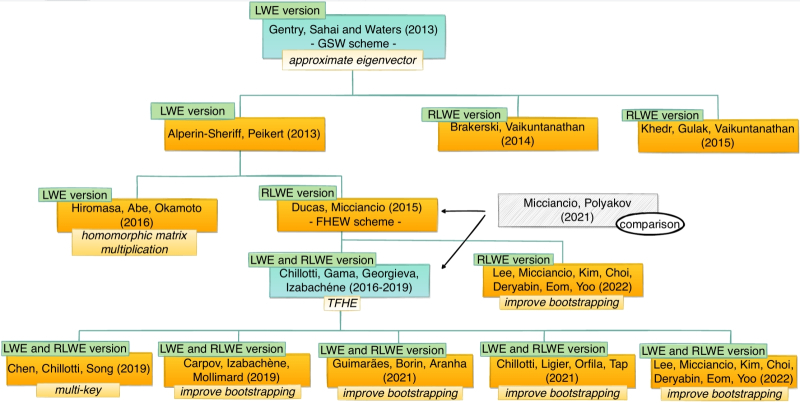

Начало третьему поколению схем FHE положила вышедшая в 2013 г. работа самого Джентри в соавторстве с Амитом Сахаем (Amit Sahai) и Брентом Уотерсом (Brent Waters) Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based, в которой за основу взяли решение задачи LWE — однако развитием её стали схемы как с использованием RLWE, так и комбинированные (источник: IEEE)

⇡#Аппаратное недоверие

Но раз FHE открывает настолько радужные перспективы в плане безопасного оперирования зашифрованными сообщениями, почему же до сих пор на него не перешли целиком и полностью; по крайней мере, в наиболее чувствительных отраслях — связанных с персональными данными, например? Ответ тривиален: слишком ресурсоёмко. Одна и та же операция с полностью открытыми данными и с теми, что закодированы по схеме FHE, во втором случае занимает на 4-5 десятичных порядков больше времени, чем в первом, если исполнять её на классических фон-неймановских серверах, где вычисления производит центральный процессор, а данные хранятся в оперативной памяти. По этой причине криптографы двигаются сегодня примерно тем же путём, что и разработчики генеративных моделей искусственного интеллекта, — переориентируются на специализированные аппаратные платформы. Однако ИИ-проектам отличным подспорьем стали серверные графические ускорители — там ведь нужно всего лишь производить взвешенное суммирование; всё сводится к перемножению матриц (хотя это может быть и не точно), и притом операнды сравнительно небольшие — представимые в 16-, 8-, а то и 4-разрядной кодировке с плавающей запятой. FHE-вычисления же приходится производить с очень длинными числами, до тысяч бит на каждое, причём округление к ним неприменимо — и так необходимо бороться с накапливающимися регулярно ошибками. Так что без специализированных вычислителей тут никак не обойтись.

Ещё один аргумент в пользу ускорения работ над аппаратной реализацией FHE — квантовая криптостойкость этой схемы кодирования. Криптография на основе решёток (lattice-based cryptography), подвидом которой можно считать FHE уже в исходной версии Джентри, устойчива к потенциальному взлому пока ещё не реализованными существенно многокубитными (имеются в виду логические кубиты, кстати, каждый из которых приходится на текущем уровне развития технологий реализовывать множеством, до нескольких сотен, физических) квантовыми системами, в отличие от подавляющего большинства широко распространённых ныне схем шифрования. Насколько эта задача важна, показывает активность известного американского агентства DARPA (благодаря которому, когда оно ещё называлось ARPA, появилась и сама сеть Internet — в исходной версии называвшаяся Arpanet). Именно это оборонное агентство инициировало в 2021 г. программу Data Protection in Virtual Environments (DPRIVE) для разработки аппаратного FHE-ускорителя. Измеримая цель, поставленная в рамках DPRIVE перед исследователями, — сократить исполнение операционных циклов в рамках FHE от десятков минут, что для начала 2010-х и серийных фон-неймановских серверов было нормально, до единиц миллисекунд. За работу взялись три группы инженеров и кибернетиков, возглавленные компаниями Duality Technologies, Galois и Intel.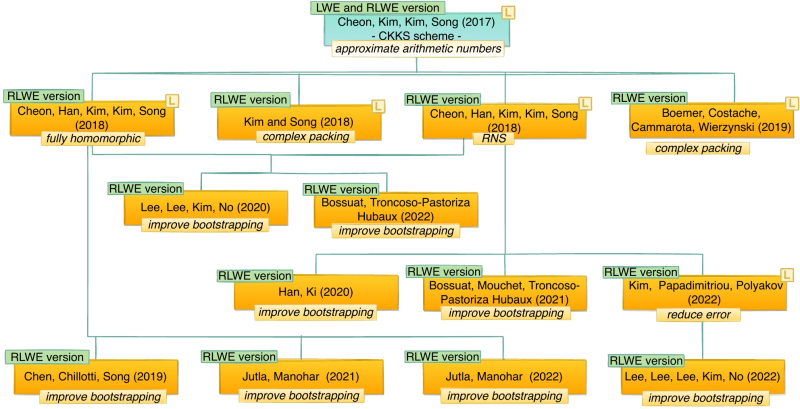

С 2017 г. мэйнстримом в области FHE стала предложенная Чун Хе Чхоном (Jung Hee Cheon), Эндрю Кимом (Andrey Kim), Миран Ким (Miran Kim) и Ёнсо Соном (Yongsoo Song) в работе Homomorphic Encryption for Arithmetic of Approximate Numbers схема, базирующаяся на совместном использовании LWE и RLWE, — но последователи их в основном сосредоточили свои усилия на «чистых» RLWE-разработках (источник: IEEE)

С 2017 г. мейнстримом в области FHE стала предложенная Чун Хе Чхоном (Jung Hee Cheon), Эндрю Кимом (Andrey Kim), Миран Ким (Miran Kim) и Ёнсо Соном (Yongsoo Song) в работе Homomorphic Encryption for Arithmetic of Approximate Numbers схема, базирующаяся на совместном использовании LWE и RLWE, но последователи их в основном сосредоточили свои усилия на «чистых» RLWE-разработках (источник: IEEE)

Galois (точнее, отделившаяся от неё Niobium) представила BASALISC — выполненный по «12-нм» технологической норме RISC-ускоритель в формате карты расширения с микросхемой PCIe площадью 150 мм². Здесь реализована четырёхуровневая иерархия интегрированной памяти, внутренний слой которой за счёт предельной близости к вычислительным ядрам и использования сверхширокой шины обеспечивает пропускную способность на уровне 32 Тбит/с. Параллельно со специализированным чипом были разработаны предназначенный для работы с ним компилятор и вспомогательное ПО. В итоге, по заверениям создателей BASALISC, на стандартных для проверки эффективности FHE-вычислений тестах он продемонстрировал сокращение времени обработки задач на 3,5 десятичных порядка (примерно в 5 тыс. раз) по сравнению с программной эмуляцией полностью гомоморфного операционного шифрования на стандартных серийных серверах.

Команда Intel тоже решила набирать название своего FHE-чипа, не отпуская клавиши Shift, — и нарекла его HERACLES. Информации об этой микросхеме в открытых источниках немного: известно, что построена она также на принципах предельно близкого расположения внушительных объёмов быстрой памяти к вычислительным ядрам (near-memory computer architecture), иерархичной структуры этой самой памяти и тоже смонтирована на карте расширения с интерфейсом PCIe. Аппаратно-программная особенность «Геракла» — архитектура полиномиального набора инструкций, Polynomial Instructions Set Architecture (P-ISA): в её рамках вводится новый тип данных, Polynomial Data, ранее в инструкциях центральных процессоров и иных вычислительных контуров не применявшийся. Благодаря P-ISA разработчикам удалось, как они утверждают, значительно ускорить операции с крупными полиномами в согласии с активно применяемым в параллельных вычислениях принципом SIMD — Single Instruction, Multiple Data. Вычислительный узел в SIMD-подходе оперирует с данными в виде векторов (на уровне инструкций, конечно же, — на фон-неймановских сумматорах всё равно складываются отдельные биты), что заметно снижает латентность в ходе решения соответствующих задач, и криптография — как раз в их числе.

Duality Technologies и примкнувшие к ней разработчики тоже не двинулись поперёк ALL_CAPS-тренда: их ASIC-сопроцессор для FHE-вычислений носит название TREBUCHET и представляет собой модульное арифметически-логическое устройство, оптимизированное для работы с длинными целыми числами (вплоть до 4096-битовой кодировки — правда, на начальном этапе реализуется 128-битовое представление) и mod-операциями, что как раз оптимально подходит для полностью гомоморфного шифрования. Интересная особенность этого проекта — ориентация на совместимость с opensource-библиотеками вроде PALISADE и OpenFHE, которые применяются уже не первый год для решения FHE-задач на компьютерах классической архитектуры.

Первым делом перспективный стартап должен отрендерить внешний вид своего всё ещё проектируемого FHE-ускорителя — надо же чем-то инвесторов привлекать? (Источник: Fabric Cryptography)

Впрочем, тремя группами фаворитов проекта DPRIVE дело не ограничивается: стартап Fabric Cryptography разрабатывает оптический FHE-ускоритель под названием Verifiable Processing Unit (VPU), который, впрочем, благодаря своей гибкой архитектуре и обширному набору инструкций с равным успехом, как полагают его проектировщики, сможет исполнять и другие схожие задачи, для которых скорость векторного умножения принципиальна: вычисления для блокчейна и криптовалют, тренировку генеративных ИИ-моделей и т. д. Компания Cornami использует более традиционные полупроводниковые микросхемы, но с программно-определяемыми и динамически реконфигурируемыми контурами на основе фирменной асинхронной архитектуры FracTLcore Compute Fabric, которая также (по крайней мере, теоретически) отменно годится для организации и FHE, и машинного обучения. Словом, поскольку к реализации полностью гомоморфного шифрования ведут, похоже, те же самые дороги, что и к дальнейшему совершенствованию прикладных аспектов генеративного ИИ, инвестиций эти изыскания привлекут немало — и практические результаты, хочется верить, тоже не заставят себя долго ждать.