Квантовая коррекция: гонка за экспонентой / Offсянка

В конце 2025 г. американский президент Дональд Трамп (Donald Trump) выразил намерение наладить частичное финансирование компаний — разработчиков квантовых вычислений из федерального бюджета; примерно по той же схеме, по которой в середине того же года государство решило стать миноритарным акционером Intel. Речь идёт о наиболее заметно продвинувшихся на этом направлении компаниях, в числе которых — IonQ, Rigetti Computing, D-Wave Quantum, Quantum Computing и Atom Computing. Их представители в основном приняли эту новость с воодушевлением: любые перспективные изыскания в ИТ-отрасли требуют изрядных инвестиций с неопределёнными сроками возврата вложенных средств, а уж создание реальных квантовых вычислителей и подавно. Тем более что мало просто научиться создавать и на продолжительное время запутывать между собой значительное число кубитов: необходимо ещё и эффективно исправлять неизбежно накапливающиеся в процессе работы таких систем ошибки. Один из способов действенной коррекции ошибок в ходе квантовых вычислений, предложенную IBM низкоплотную проверку чётности, мы недавно рассматривали; теперь пришёл черёд изучить практикуемые другими исследователями методы.

Реализующий квантовую запутанность логический вентиль во вдохновенном представлении художника (источник: University of Sydney)

⇡#Розетта беспокоит

В самом конце XVIII в. в Египте был обнаружен артефакт, давший ключ к расшифровке иероглифической письменности, — Розеттский камень с одним и тем же текстом, записанным трижды: древнеегипетскими иероглифами, более поздним демотическим письмом и по-древнегречески. С тех пор «розеттскими камнями» в науке и технике стали называть находки, позволяющие по некоторой удачной аналогии понять — а затем, разобравшись в понятом, и воспроизвести — нечто ранее недоступное. Вот и квантовый логический вентиль, продемонстрированный в августе 2025 г. исследователями из Лаборатории квантового контроля при Наноинституте Сиднейского университета (Quantum Control Laboratory at the University of Sydney Nano Institute) назвали «розеттским камнем квантовых вычислений» — потому что он позволяет (по крайней мере, в теории) радикально сократить число физических кубитов, необходимых для создания одного логического. Напомним, что как раз в 2026 г. IBM планирует ввести в строй 12-кубитный квантовый компьютер, построенный на 288 физических трансмонах и производящий вычисления с погрешностью не более 0,1%, — т. е. каждый логический кубит потребует здесь для своей реализации 24 физических, организованных в весьма непростую исправляющую ошибки схему. И это вполне обоснованно преподносится как немалое достижение: если аналогичный вычислитель создавать на основе поверхностного алгоритма коррекции ошибок (применяемого, например, Google в своей серии квантовых вычислителей Willow), то, чтобы сформировать ту же дюжину логических кубитов и достичь схожей погрешности вычислений, понадобится уже почти 3 тыс. физических — на десятичный порядок больше.

Квантовый вычислительный контур по аналогии с классическим состоит из некоторого количества соединённых в определённом порядке вентилей; прохождение сигналов по этому контуру и производит, собственно, вычисление. Вентиль можно, отвлекаясь от физической его реализации, представить как некий оператор, по установленным правилам преобразующий сигнал(ы) на входе в сигнал(ы) на выходе (тут важно подчеркнуть, что количество входов и выходов у квантовых вентилей должно совпадать в силу требования унитарности). В случае квантовых вычислений сигналами служат состояния конкретных кубитов, принимающих участие в вычислениях. Но на протяжении всего процесса вычислений кубиты обязаны оставаться квантовыми объектами, т. е. сохранять состояние суперпозиции, не коллапсируя ни в одно из предельных — |0⟩ или |1⟩. Потому и квантовые вентили, подразумевающие операции с двумя кубитами и более, должны запутывать эти самые кубиты (entangling logic gates) — т. е. формировать квантовые корреляции между своими операндами, чтобы измерение состояния одного из запутанных кубитов моментально и однозначно определяло бы состояние другого. Базовый пример запутывающего вентиля — контролируемое отрицание (controlled NOT; CNOT): операндами для него выступают два кубита — целевой и контролирующий. Если контролирующий коллапсирует в состояние |1⟩, то целевой тут же должен принять состояние, обратное своему исходному, каким бы то ни было. Напомним в очередной раз, что все операции внутри квантового вычислительного контура, пока тот остаётся в состоянии суперпозиции, целиком и полностью обратимы, и потому говорить о том, что CNOT «меняет состояние целевого кубита на обратное», не совсем корректно: в итоге поменяет, да, — но пока квантовая неопределённость не разрешена, в состоянии суперпозиции квантово запутанной системы сокрыты все в принципе доступные возможности.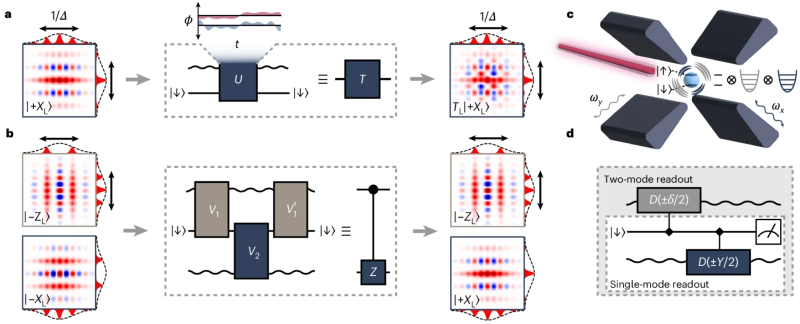

Иллюстрация из обсуждаемой статьи в Nature Physics, на которой показаны: реализация однокубитного (a) и двухкубитного (b) вентилей на захваченном в ловушку ионе иттербия (c), а также схема проведения одно- и двухмодовых измерений по протоколу GKP (d) (источник: University of Sydney)

Суть запутывающего квантового вентиля, который предложили исследователи из Сиднея, в том, что он реализует протокол Готтесмана – Китаева – Прескилла (Gottesman – Kitaev – Preskill code; GKP), названный так в честь Дэниела Готтесмана, Алексея Китаева и Джона Прескилла, которые опубликовали соответствующую работу в 2001 году. Сравнение GKP с Розеттским камнем имеет смысл постольку, поскольку этот протокол создаёт точное представление кубитов, — точнее, любых квантовых систем, размерность гильбертова пространства которых конечна, — в другой квантовой системе, представленной, например, осцилляторами; переводит, образно говоря, древнеегипетскую иероглифическую запись на классический греческий без искажения закодированного в первой сообщения. В основу протокола положены так называемые решётчатые состояния, инвариантные относительно сдвига на фиксированную величину: такая повторяющаяся «решётчатость» позволяет с лёгкостью обнаруживать и затем исправлять небольшие ошибки сдвига состояний кубита. Получается, одно должным образом сконструированное решётчатое состояние — т. е. корректно подобранный порождающий его оператор смещения — заменяет собой целый сонм контролирующих кубитов, которые необходимо было бы запутывать с исходным для непрерывного контроля его состояния. Правда, в данном случае уход от физической избыточности по числу необходимых кубитов (для реализации одного-единственного логического) производится за счёт построения довольно сложной системы, которая в принципе способна хранить информацию об осцилляциях (колебательных состояниях) кубитов, — с применением бозонных кодов. Иными словами, далеко не всякая квантовая система допускает коррекцию с применением GKP, — да и не любые ошибки этот протокол способен исправлять, а только сравнительно малые.

Группа исследователей из Сиднея поместила в ловушку Пауля (Paul trap) изолированный ион иттербия, энергетическое состояние которого характеризуется естественным спектром колебаний (осцилляций), — а тот, в свою очередь, возникает в результате взаимодействия собственного электромагнитного поля этой частицы с внешним полем, удерживающим её внутри определённой области пространства. Спектр этот выходит дискретным, что и позволяет закодировать в получившемся гармоническом осцилляторе сперва один кубит по протоколу GKP, а затем и второй: поскольку ион в ловушке колеблется в трёх измерениях, его смещение по каждому из них можно рассматривать как отдельное квантовое состояние, а так как ион тот же самый — колебания по двум измерениям выходят естественным образом запутанными. В квантовой механике гармонические осцилляторы и бозоны (частицы, подчиняющиеся статистике Бозе — Эйнштейна) описываются схожими операторами, и потому подобные схемы обработки квантовой информации — использующие бесконечномерные гильбертовы пространства гармонических осцилляторов для кодирования логических кубитов с возможностью коррекции ошибок — называют бозонными. Помимо механических колебаний захваченных ионов, на которые сделала ставку группа из Сиднея, бозонные схемы возможно реализовать, в частности, на электромагнитных модах в микроволновых резонаторах и на оптических фотонах. Тем не менее определённая специфичность такого подхода, а именно использование гармонических осцилляторов, затрудняет создание в рамках протокола GKP универсального набора вентилей для квантовых операций. Так что даже если предложенная исследователями лабораторная установка эволюционирует со временем в работоспособный квантовый компьютер, круг в принципе решаемых на нём задач окажется ещё более узким, чем тот, что в принципе охватывают квантовые алгоритмы. Впрочем, существенный плюс предложенного исследователями подхода — в отсутствии необходимости криогенного охлаждения установки: ион иттербия удерживается внутри ловушки Пауля лазерами при комнатной температуре.

Собственно ловушка Пауля представляет собой группу электродов, размещённых внутри показанной здесь вакуумированной камеры. Если такими окажутся габариты одного-единственного вентиля перспективного (не нуждающегося в дополнительных корректирующих кубитах) квантового компьютера, готовая к решению практических задач конструкция — логических кубитов этак на тысячу — выйдет поистине монструозной (источник: Wikimedia Commons)

⇡#Это просто магия!

Квантовые явления принципиально отличаются от феноменов макромира, доступных нам в непосредственных ощущениях: достаточно упомянуть нелокальность проявления квантовой запутанности, т. е. мгновенное (не ограниченное скоростью света, предельной для нашей Вселенной, а моментальное) схлопывание состояния одного из пары предварительно запутанных квантовых объектов ровно тогда же, когда состояние второго измерено, — на каком бы расстоянии эти объекты ни находились. Вот почему эмуляция квантовых вычислителей на классических компьютерах не просто сложна, но — начиная с определённого уровня глубины — недостоверна: алгоритмически исчерпывающе запрограммировать физически корректные проявления квантовых эффектов в по-настоящему сложных системах попросту невозможно. Понятно теперь, отчего, описывая наиболее перспективные квантовые компьютеры, исследователи говорят о волшебных состояниях (magic states). Это такие особенные конфигурации квантовых систем, которые классическими средствами принципиально не удастся воспроизвести, сколько ни бейся, — и как раз благодаря которым всё-таки будет (как ожидается) однажды достигнуто квантовое превосходство над сколь угодно сложными полупроводниковыми вычислителями.

Упомянутый ранее вентиль CNOT, подробно расписанный в предыдущей статье о квантовой коррекции ошибок поверхностный код и ещё целый ряд операций, широко применяемых сегодня разработчиками квантовых компьютеров, относятся к так называемым клиффордовым вентилям (Clifford gates): с одной стороны, вполне действенным для исполнения важных квантово-вычислительных операций (запутывания кубитов, коррекции ошибок и т. д.), а с другой — не таким уж и квантовым, если присмотреться повнимательней. Точнее, вентили эти настолько удачно опрощают — лишают магического ореола непривычности, отсутствия прямых аналогий с макроскопическими явлениями — взаимодействие квантовых объектов, что операции с их участием великолепно эмулируются самыми обычными классическими компьютерами. Да, с чудовищным расходованием времени, энергии и аппаратных ресурсов; но квантовое превосходство клиффордовых вычислителей (Clifford circuits) над привычными полупроводниковыми — исключительно количественное; притом не самое великое. Формально — никакого жульничества: аппаратные клиффордовы вычислители действительно производят квантовые операции над самыми настоящими кубитами и получают результат куда быстрее, чем если бы аналогичная задача решалась на классическом компьютере. Однако фундаментальная теорема Готтесмана – Книлла (Gottesman-Knill theorem) утверждает, что любое квантовое вычисление, составленное из клиффордовых операций, можно осуществить и на классическом компьютере — за полиномиальное время. Иными словами, ставка на одни только клиффордовы вентили позволяет получить лишь необратимый квантовый компьютер — в некотором смысле аналог классического, для которого жёстко задана стрела времени; задана самим фактом того, что вычисления, как предполагают его создатели, могут порождать ошибки, которые, в свою очередь, можно исправлять, фактически возвращая систему в предшествующее состояние для перерасчёта. Но на квантовом уровне процессы полностью симметричны относительно выбора направления, в котором течёт время; следовательно, универсальный квантовый вычислитель, как мы уже не раз подчёркивали, должен быть целиком и полностью обратим — до тех пор, пока не получен определённый результат, т. е. пока не произошёл коллапс волновой функции.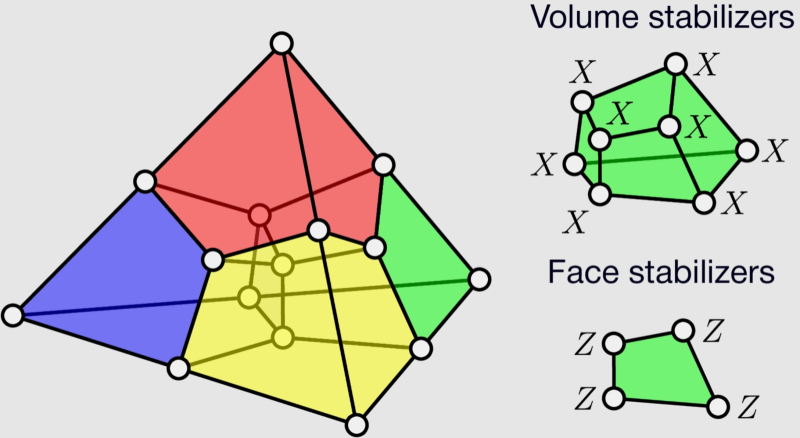

Геометрическое представление квантового кода Рида – Мюллера (Reed-Muller code), посредством которого 15 физических кубитов формируют один логический с дистанцией 3 (distance-3, или просто d3, — т. е. с возможностью обнаруживать и исправлять одну ошибку). Это минимальный по числу компонентов d3-код, позволяющий создать неклиффордов T-вентиль, и он чаще прочих схем используется при дистилляции волшебных состояний (источник: arxiv.org/abs/2507.12511)

Чем же плохи клиффордовы вентили? Ведь, в конце-то концов, если полупроводниковая эмуляция квантового вычислителя на их основе будет биться над некой задачей десятки лет, а аппаратный 1000-кубитный компьютер решит её за пару месяцев (а не за пару минут, как было бы, обеспечивай он экспоненциальный выигрыш по времени, а не полиномиальный), какая разница, универсален он или нет? Для тех, чью область интересов решённая задача непосредственно затрагивает (для криптографов, например, которым в любом случае придётся отказываться от RSA-шифрования), разница и впрямь невелика. Но круг алгоритмов, успешно исполняемых на клиффордовых вычислителях, не так уж обширен — и, самое главное, добиться экспоненциального выигрыша во времени там, где его пока нет, очень уж хочется. Освежим на всякий случай в памяти смысл универсального многокубитного квантового компьютера: если число находящихся в состоянии суперпозиции кубитов в нём — L, то общее количество линейно независимых состояний такой системы — 2^L. И весь процесс вычисления на таком компьютере сводится, по сути, к одному-единственному повороту вектора состояния в гильбертовом пространстве размерности 2^L. А чтобы такой поворот реализовать, необходимо весьма свободно оперировать состояниями запутанных кубитов. И если S-вентиль (фазовый вентиль), который поворачивает вектор состояния одиночного кубита на сфере Блоха на 90° относительно оси Z, относится к клиффордовым, то T-вентиль, тоже реализующий поворот, но лишь на 45°, — уже нет. Найти физическую реализацию T-вентиля вполне возможно, но вот загвоздка: воплотить для него столь же надёжную (пусть и громоздкую) систему коррекции ошибок, что применима к клиффордовым вентилям, уже не удастся. Не той он системы!

Два с лишним десятка лет назад Эмануэль Книлл (Emanuel Knill), соавтор той самой теоремы Готтесмана – Книлла и один из столпов всей современной теории квантовых вычислений, выдвинул идею квантовых вычислений с постселективным отбором. Предлагалось отыскать такую фильтрующую схему — квантовую же, разумеется; органично интегрируемую в квантовый компьютер, — которая принимала бы выходные данные (в том числе поступающие через зашумлённые вентили) для дальнейшей их обработки только в том случае, если результаты измерений удовлетворяют заранее заданным условиям. В качестве фильтрующей схемы должны были выступать вспомогательные кубиты, заблаговременно приведённые в такое — волшебное — состояние (magic state), что, когда они транслируют это своё состояние клиффордову вентилю, результат оказывается в точности таким же, как если бы на его вход поступил результат выполнения неклиффордовой операции (того же T-поворота, например). В результате вся система вновь оказывается клиффордовой (правда, как именно реализовывать работоспособные волшебные логические кубиты, Книлл не уточнял), к ней вновь оказываются применимы алгоритмы коррекции ошибок, — но теперь выигрыш её по скорости работы в сравнении с фоннеймановским компьютером значительно ближе к экспоненциальному, чем к полиномиальному. Именно ближе, поскольку необходимость исправлять выявленные ошибки всё равно тормозит вычисления, — но это всё-таки ощутимый прогресс.

Прибор для дистилляции волшебных состояний — на основе Gemini, квантового компьютера, использующего в качестве кубитов нейтральные атомы (источник: QuEra)

⇡#Затратное удовольствие

Волшебные, или магические, состояния, таким образом, — это подготовленные заранее квантовые состояния, которые затем используются в качестве ресурсов (катализаторов, грубо говоря) более сложными, почти уже универсальными, квантовыми алгоритмами для выполнения тех на клиффордовых системах. Сам же процесс подготовки таких состояний называется их дистилляцией (magic state distillation). В середине 2025 г. в компании QuEra Computing со штаб-квартирой в Бостоне, штат Массачусетс, продемонстрировали на практике дистилляцию волшебных состояний на логических, что важно, кубитах, — т. е. предметно засвидетельствовали принципиальную достижимость намеченной ещё Книллом цели: произвести качественный скачок от полиномиального к экспоненциальному выигрышу по времени при использовании квантовых компьютеров. Тут важно пояснить, что сама по себе процедура дистилляции на физических кубитах была реализована значительно ранее; достижение же QuEra в адаптации её именно для логических, представленных целой группой взаимно запутанных физических. Типичная частота появления ошибок в квантовых вычислениях до этого момента составляла в лучшем случае 10⁻³: одна ошибка на тысячу операций. Применение же дистилляции волшебных состояний позволило, как утверждают исследователи, разом улучшить этот результат до 10⁻⁹. И хотя отставание от характерных для полупроводниковых компьютеров величин по-прежнему огромно, от 8 до 10 десятичных порядков, всё-таки пресловутое квантовое превосходство буквально в один момент обрело существенно более реалистичные контуры.

За счёт чего же реализуется, собственно, «магия» волшебных состояний? Magic упоминается в данном случае физиками вовсе не для красного словца: квантовые феномены действительно настолько непривычны с точки зрения нашего, макроскопического опыта, что под почерпнутое из сказок определение чудесного вполне подходят. Ещё из школьного курса всем наверняка памятно влияние наблюдателя (в широком смысле, как некоего регистрирующего квантовые состояния устройства; не обязательно живого разумного существа) на квантовые процессы: элементарная частица ведёт себя как волна или как корпускула — в зависимости от того, какие её свойства в данный момент фиксируются. Хорошо известен и принцип неопределённости Гейзенберга: невозможно одновременно точно измерить некоторые связанные параметры квантового объекта — координаты и импульса, силы тока и напряжения, величин напряжённости электрического и магнитного полей. Однако этим дело не ограничивается: оказывается, сами измерения различных свойств квантовых объектов не могут рассматриваться просто как независимые фиксации объективно существующих, однозначных значений. Грубо говоря, первое измерение уже меняет состояние квантовой системы, и потому значение второго (пусть измеряется при этом совершенно иная характеристика) неизбежно будет зависеть от того, какой результат получен при первом, — это называют квантовой контекстуальностью. Результат измерения данной величины в квантовом мире зависит от выбора других, измеряемых одновременно с нею — и образующих тем самым контекст измерения.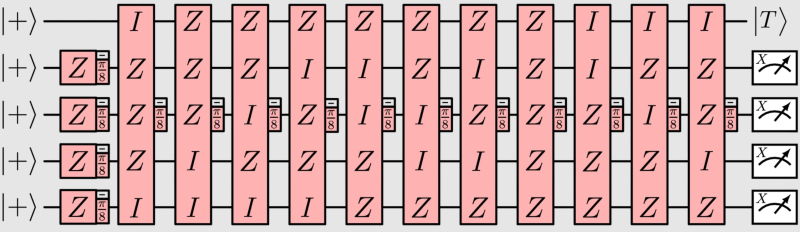

Один из возможных протоколов дистилляции с применением 5 логических кубитов. Каждый вентиль соответствует одно- или многокубитному вращению, которое может быть реализовано с использованием одного-единственного исходного состояния |T⟩. После выполнения 15 таких вращений значения четырёх стабилизаторов X-типа кода Рида – Мюллера вычисляются по результатам измерений логических кубитов с 2-го по 5-й в базисе X. Если все результаты измерений равны +1, дистилляция успешна, и первый логический кубит находится в состоянии |T⟩ (источник: arxiv.org/abs/2507.12511)

Квантовая контекстуальность — вполне магическое по нашим (классическим) меркам свойство; своего рода неклассическая корреляция независимых (вроде бы, по привычной нам логике) физических величин. Волшебные состояния имеют к ней самое прямое отношение: они существуют объективно (поскольку могут быть зафиксированы приборами), но не описываются классическими моделями, — и как раз потому к ним не применимы клиффордовы вентили. Учёт «отдалённости» волшебного состояния от того, что поддаётся воспроизведению классическими средствами, — многие исследователи иронично называют меру такой отдалённости «квантовой маной» (quantum mana), — как раз и позволяет квантовым вычислениям освободиться от оков классической имитации, налагаемых необходимостью применять исключительно клиффордовы вычислители ради возможности исправлять неизбежно возникающие ошибки. Неизбежность же эта обусловлена вполне объективно: границы квантового мира чрезвычайно узки (привязаны к характерным размерам единичных элементарных частиц, в крайнем случае атомов и молекул), тогда как квантовые компьютеры поневоле макроскопичны. Именно несоответствие масштабов производящих квантовые вычисления систем и тех их элементов, к которым, собственно, применимы в полной мере закономерности квантового мира, и порождает серьёзные технические проблемы, которые исследователям приходится столь мучительно преодолевать.

Буквально в двух словах: волшебные состояния, даром что «магические» по своей квантовой природе, возникают вовсе не по мановению некой нанопалочки: они формируются в пределах квантового же компьютера примерно теми же средствами, какими инженеры выстраивают уже привычные квантовые контуры. На качественном уровне всё довольно прозрачно: любой отдельный физический кубит неизбежно будет «шуметь», однако если создать достаточное количество его копий, то процедура дистилляции, описанная вчерне Эмануэлем Книллом, а чуть позже детализированная в работе Сергея Бравого и Алексея Китаева (Sergei Bravyi, Alexei Kitaev), позволит за счёт разительного сокращения их числа получить небольшую партию практически «чистых», не содержащих паразитных шумов кубитов. Это фактически тоже коррекция ошибок — но на уровне состояний, а не операций; причём многократное повторение дистилляции (правда, с экспоненциальным ростом числа исходных копий, — опять ресурсозатраты!) даёт возможность снизить частоту ошибок волшебного состояния до произвольно низкого уровня. И это — настоящая находка! Юваль Богер (Yuval Boger), коммерческий директор QuEra, утверждал, что в отсутствие дистилляции волшебных состояний квантовые компьютеры вовсе не имеют шанса исполнить своё предназначение (под которым, очевидно, подразумевается как раз выход на экспоненциальное сокращение продолжительности вычислений), и с ним очень многие солидарны.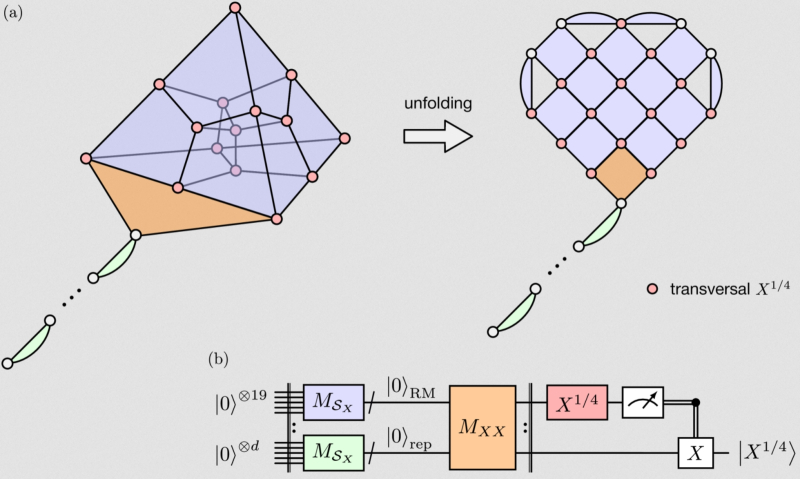

Пример развёртки группы стабилизаторов X-типа для квантовой коррекции ошибок с использованием кода Рида – Мюллера в двумерную матрицу. Связи между соседними узлами обеспечивают четыре дополнительных кубита, а также стабилизаторы с весом 2 (d2). Код повторения, который будет содержать выходное волшебное состояние (зелёная заливка), объединяется с развёрткой через процедуру совместного измерения (оранжевая заливка) (источник: arxiv.org/abs/2507.12511)

Хотя с момента публикации, описывающей достижение QuEra в Nature, прошло не так много времени, дистилляция волшебных состояний успела сделаться краеугольным камнем большинства новых отказоустойчивых архитектур квантовых компьютеров. Правда, возникла другая напасть: теперь нередко бóльшая часть ресурсов, затрачиваемых на разработку очередного квантового алгоритма, уходит на дистилляцию магических состояний. Сами первопроходцы ограничились созданием пяти вспомогательных зашумлённых кубитов, из которых по алгоритму дистилляции был получен один носитель волшебного состояния на логическом уровне, — таким образом впервые была продемонстрирована принципиальная возможность применения дистилляции к клиффордовой системе. Примерно тогда же разработчики из Quantinuum отчитались об успешном формировании — тоже с использованием дистилляции волшебных состояний — такого логического T-вентиля (тот самый поворот на 45° на сфере Блоха), что превзошёл по точности исполнения операций любой известный ныне физический T-вентиль. Компания Alice & Bob, разработчики знакомых нашим читателям кошачьих кубитов, реализовали целую структурную схему для дистилляции волшебных состояний. В результате на квантовом компьютере, где всего лишь 53 физических кубита пошли на формирование этой «магии», им удалось достичь точности вычислений 10⁻⁶ — для чего без этой схемы потребовалось бы около полутысячи физических кубитов. И это, судя по всему, только начало: дистилляция волшебных состояний обещает вдохнуть новую жизнь по крайней мере в квантовые компьютеры на природных квантовых объектах (нейтральных атомах, ионах и т. п.), тогда как системы на макроскопической аппаратной базе вроде трансмонов воспользоваться этой лазейкой для повышения своей производительности не могут — во всяком случае, пока. Кто знает, вдруг магический квантовый сопроцессор-дистиллятор научатся сопрягать с кубитами совершенно иной физической природы? Вот тогда прогресс квантовых вычислений ускорился бы поистине неимоверно!