Опрос
|
реклама
Быстрый переход
Российский математик нашел ключ к «нерешаемым» уравнениям XIX века: это упростит расчеты в физике и космонавтике
27.01.2026 [19:38],
Геннадий Детинич
Национальный исследовательский университет «Высшая школа экономики» (НИУ ВШЭ) сообщил, что математик Иван Ремизов из Нижнего Новгорода нашёл возможность для условно простого решения дифференциальных уравнений второго порядка с переменными коэффициентами. На протяжении почти двух столетий такие уравнения считались нерешаемыми. Между тем, они играют ключевую роль в математике и естественных науках, поскольку используются для описания динамических процессов. 
Источник изображения: ИИ-генерация ChatGPT 5.2/3DNews Исторически ограничение было связано с результатами французского математика Жозефа Лиувилля, который ещё в 1834 году показал, что решения подобных уравнений нельзя выразить через конечное число стандартных операций и элементарных функций. Из-за этого математики были вынуждены либо искать частные решения, либо использовать приближения, что исключало универсальную методику и очень сильно усложняло расчёты. Иными словами, общей формулы, в которую можно просто подставить «циферки» и получить решение, не существовало. Иван Ремизов предложил новый подход, расширив класс допустимых математических операций. Он не стал спорить с Лиувиллем, а просто добавил в уравнения ещё один математический инструмент — нахождение предела последовательности. Для этого математик воспользовался теорией Чернова и преобразованием Лапласа. Это позволило ему выстроить универсальную формулу, которая формально даёт решение любого уравнения «нерешаемого» класса, обходя классические ограничения теории. «Суть идеи в том, что сложный, постоянно меняющийся процесс разбивается на бесконечное множество простых шагов. Для каждого такого участка строится свое приближение — элементарный фрагмент, который описывает поведение системы в конкретной точке. По отдельности эти кусочки дают лишь упрощенную картину, но, когда их число устремляется к бесконечности, они бесшовно соединяются в идеально точный график решения», — поясняется в пресс-релизе НИУ ВШЭ. «Дифференциальные уравнения второго порядка используются не только для моделирования событий реального мира, но и для определения новых функций, которые нельзя задать иным образом. К ним относятся, например, так называемые специальные функции Матье и Хилла, они критически важны для понимания того, как движутся спутники на орбите или протоны в Большом адронном коллайдере». Чуть более сложным математическим языком об открытии можно прочитать на сайте НИУ ВШЭ. На английском языке работа опубликована полностью во «Владикавказском математическом журнале». ИИ-модели начали щёлкать сложные математические задачи
15.01.2026 [13:35],
Павел Котов
В минувшие выходные инженер-программист Нил Сомани (Neel Somani) тестировал математические способности новой модели искусственного интеллекта OpenAI и сделал неожиданное открытие. Он поставил ChatGPT сложнейшую математическую задачу, дал чат-боту подумать 15 минут и получил готовое решение. 
Источник изображения: Thomas T / unsplash.com Исследователь оценил доказательство, провёл его формализацию при помощи средства от Harmonic, и всё оказалось в порядке. Ещё больше его впечатлила цепочка рассуждений ChatGPT — в ней ИИ воспроизвёл формулу Лежандра, постулат Бертрана и теорему о звезде Давида; а также нашёл на Math Overflow сообщение от 2013 года, где приводилось решение аналогичной задачи. Окончательный вариант от ChatGPT имел существенные отличия от образца и давал полное решение версии одной из задач, поставленных легендарным математиком Палом Эрдёшем (Pál Erdős) — его коллекция нерешённых задач сейчас превратилась в полигон для ИИ. Этот удивительный результат не уникален — модели ИИ теперь повсеместно применяются в математике: средства «глубокого исследования» OpenAI отвечают за обзор литературы, а Harmonic Aristotle производит формализацию доказательств. Модель OpenAI GPT-5.2, по словам Нила Сомани, оказалась искуснее в рассуждениях, чем предыдущие версии — они уже научились решать остававшиеся открытыми задачи, по сути, расширяя границы человеческих знаний. Пал Эрдёш оставил после себя более тысячи гипотез, которые зафиксированы сообществом математиков в Сети — и они обнаружили, что GPT-5.2 на удивление хорошо справляется со сложнейшими математическими задачами. В период с 25 декабря 2025 года и по настоящий момент решены 15 задач Эрдёша, и в работе над 11 из них участвовал ИИ. Авторитетный математик Теренс Тао (Terence Tao) привёл восемь задач Эрдёша, в которых ИИ добился значительного прогресса; ещё в шести случаях его удалось достичь за счёт поиска и дальнейшего развития ранних исследований. Совсем без участия человека ИИ с ними пока не справился бы, но его роль становится более важной. «Таким образом, многие из этих более простых задач Эрдёша теперь с большей вероятностью могут решаться исключительно основанными на ИИ методами, чем человеческими или гибридными средствами», — делает вывод Теренс Тао. Ещё один важный фактор — сдвиг в сторону формализации. Это трудоёмкая задача, которая упрощает проверку и расширение математических рассуждений; она не требует ни ИИ, ни даже просто компьютеров, но сейчас появились средства, которые в значительной мере упростили этот процесс. Популярным, например, стал инструмент Lean, разработанный Microsoft Research ещё в 2013 году; средство Harmonic Aristotle позволяет в значительной мере автоматизировать эту задачу. Внезапный скачок в числе решённых задач Эрдёша привёл к тому, что упоминание сервисов Aristotle или ChatGPT добавляет материалам вескости в профессиональном сообществе. Найден новый способ поиска простых чисел — теперь RSA-шифрование устоит перед квантовыми компьютерами
21.06.2025 [21:56],
Геннадий Детинич
Издаваемый Национальной академией наук США (NAS) престижный рецензируемый журнал Proceedings of the National Academy of Sciences присудил ежегодно учреждаемую премию Cozzarelli Award группе математиков во главе с исследователем из США Кеном Оно (Ken Ono) из Университета Вирджинии. Кен с коллегами нашли прямую связь между простыми числами — основой RSA-ключей — и уравнениями 1800-летней давности, что стало прорывом в области защиты данных. 
Источник изображения: ИИ-генерация Grok 3/3DNews Открытие поможет защитить данные в эпоху квантовых компьютеров, которые скоро начнут угрожать RSA-шифрованию. Сегодня даже самые мощные классические суперкомпьютеры не способны за разумное время факторизовать достаточно большие целые числа — разложить их на простые множители для вычисления ключей шифрования. Потенциально с такой задачей начнут справляться только квантовые компьютеры за счёт явления суперпозиции, когда информация в каждом кубите будет представлена одновременно множеством состояний от 0 до 1, а не одним или другим фиксированным значением. Таким образом, учёным надо научиться находить всё большие простые числа (сейчас самое большое найденное простое число состоит из 41 млн цифр), а также искать иные подходы для определения таковых. Проделанная коллективом Кена Оно работа из таких — они нашли неизвестную ранее взаимосвязь между так называемыми диофантовыми уравнениями и простыми числами. Открытие диофантовых уравнений приписывают математику III века Диофанту Александрийскому. Они могут быть невероятно сложными, но если полученный ответ окажется верным, это означает, что число будет простым. По сути, это новый способ исследования простых чисел, который никогда ранее не использовался. «Простые числа, составляющие основу мультипликативной теории чисел, являются решениями бесконечно многих специальных “диофантовых уравнений” в хорошо изученных статистических разбиениях, — пишут авторы. — Другими словами, целочисленные разбиения позволяют находить простые числа бесконечно многими естественными способами». Проделанная учёными работа могла быть сделана 20, 30 и 80 лет назад, когда стала понятна важность шифрования данных, и в любом случае она бы произвела фурор среди специалистов. Удивительно, до сих пор её никто не делал, подчёркивают авторы исследования и добавляют, что теперь открывается возможность подключить к анализу простых чисел ряд статистических методов. Тем самым RSA-шифрование может получить второе дыхание и ещё окажет сопротивление квантовым компьютерам через пять, десять или больше лет. Учёные уличили ИИ в неспособности строить математические доказательства в олимпиадных задачах USAMO 2025 года
26.04.2025 [12:29],
Дмитрий Федоров
Новое исследование ETH Zurich и INSAIT показало, что современные ИИ-модели, имитирующие рассуждение и уверенно решающие стандартные математические задачи, практически не способны формулировать полные доказательства уровня Математической олимпиады США 2025 года (USAMO). Эти результаты ставят под сомнение возможность глубокого математического рассуждения у современных ИИ-моделей. 
Источник изображения: Imkara Visual / Unsplash В марте 2025 года исследовательская группа из Швейцарской высшей технической школы Цюриха (ETH Zurich) и Института компьютерных наук, искусственного интеллекта и технологий (INSAIT) при Софийском университете, возглавляемая Иво Петровым (Ivo Petrov) и Мартином Вечевым (Martin Vechev), опубликовала препринт научной статьи под названием «Proof or Bluff? Evaluating LLMs on 2025 USA Math Olympiad» (рус. — Доказательство или блеф? Оценка больших языковых моделей на Математической олимпиаде США 2025 года). Работа направлена на оценку способности больших языковых моделей (LLMs), имитирующих рассуждение, генерировать полные математические доказательства на олимпиадных задачах. Для анализа были использованы шесть задач с USAMO 2025 года, организованного Математической ассоциацией Америки. ИИ-модели тестировались сразу после публикации заданий для минимизации риска утечки данных в обучающие выборки. Средняя результативность по всем ИИ-моделям при генерации полных доказательств составила менее 5 % от максимально возможных баллов. Системы оценивались по шкале от 0 до 7 баллов за задачу с учётом частичных зачётов, выставляемых экспертами. Лишь одна модель — Gemini 2.5 Pro компании Google — показала заметно лучший результат, набрав 10,1 балла из 42 возможных, что эквивалентно примерно 24 %. Остальные модели существенно отставали: DeepSeek R1 и Grok 3 получили по 2,0 балла, Gemini Flash Thinking — 1,8 балла, Claude 3.7 Sonnet — 1,5 балла, Qwen QwQ и OpenAI o1-pro — по 1,2 балла. ИИ-модель o3-mini-high компании OpenAI набрала всего 0,9 балла. Из почти 200 сгенерированных решений ни одно не было оценено на максимальный балл. Исследование подчёркивает фундаментальное различие между решением задач и построением математических доказательств. Стандартные задачи, такие как вычисление значения выражения или нахождение переменной, требуют лишь конечного правильного ответа. В отличие от них, доказательства требуют последовательной логической аргументации, объясняющей истинность утверждения для всех возможных случаев. Это качественное различие делает задачи уровня USAMO значительно более требовательными к глубине рассуждения. 
Скриншот задачи №1 USAMO 2025 года и её решения на сайте AoPSOnline. Источник изображения: AoPSOnline Авторы исследования выявили характерные модели ошибок в работе ИИ. Одной из них стала неспособность поддерживать корректные логические связи на протяжении всей цепочки вывода. На примере задачи №5 USAMO 2025 года ИИ-модели должны были найти все натуральные значения k, при которых определённая сумма биномиальных коэффициентов в степени k остаётся целым числом при любом положительном n. Модель Qwen QwQ допустила грубую ошибку, исключив возможные нецелые значения, разрешённые условиями задачи, что привело к неправильному окончательному выводу, несмотря на правильное определение условий на промежуточных этапах. Характерной особенностью поведения моделей стало то, что даже в случае серьёзных логических ошибок они формулировали свои решения в утвердительной форме, без каких-либо признаков сомнения или указаний на возможные противоречия. Это свойство имитации рассуждения указывает на отсутствие у ИИ-моделей механизмов внутренней самопроверки и коррекции вывода. Авторы отметили также влияние особенностей обучения на качество решений. Тестируемые ИИ-модели демонстрировали артефакты оптимизационных стратегий, применяемых при подготовке к стандартным бенчмаркам: например, принудительное форматирование ответов с использованием команды \boxed{}, предназначенное для удобства автоматизированной проверки. Эти шаблонные подходы приводили к ошибкам в контексте задач, где требовалось развёрнутое доказательство, а не только числовой ответ.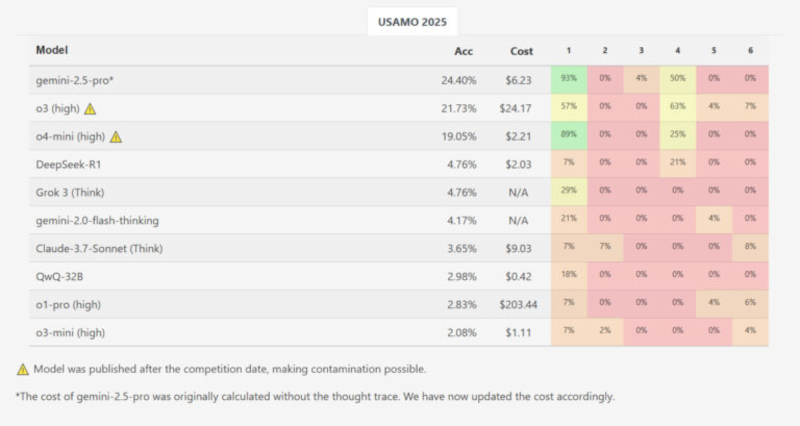 
Показатели точности ИИ-моделей на каждой задаче USAMO 2025 года. Источник изображения: MathArena Несмотря на выявленные ограничения, внедрение методов цепочки размышлений и имитации рассуждения положительно сказались на формировании промежуточных логических шагов в процессе вывода ИИ-моделей. Механизм масштабирования вычислений на этапе вывода позволяет ИИ строить более связные локальные рассуждения. Однако фундаментальная проблема остаётся: современные большие языковые модели (LLM) на архитектуре «Трансформер» (Transformer) продолжают работать как системы распознавания паттернов, а не как самостоятельные системы концептуального рассуждения. Более высокие результаты модели Gemini 2.5 Pro свидетельствуют о потенциальной возможности сокращения разрыва между симулированным и реальным рассуждением в будущем. Однако для достижения качественного прогресса необходимо обучение ИИ-моделей более глубоким многомерным связям в латентном пространстве и освоение принципов построения новых логических структур, а не только копирование существующих шаблонов из обучающих выборок. Открыто самое большое простое число — в нём 41 миллион цифр
22.10.2024 [17:01],
Павел Котов
Бывший инженер-программист Nvidia Люк Дюран (Luke Durant) и проект GIMPS (Great Internet Mersenne Prime Search) нашли самое большое на сегодняшний день известное человеку простое число, для написания которого потребуются 41 млн цифр. GIMPS — это попытка добровольцев по всему миру обнаружить простые числа Мерсенна, которые имеют вид 2n-1. 
Источник изображения: kp yamu Jayanath / pixabay.com Самое большое простое число, известное человеку на данный момент — это 2136 279 841-1; а обозначается оно как M136279841. Чтобы получить это число, потребуется умножать двойку на себя более 136 млн раз, а из получившегося результата вычесть единицу. До этого шестью годами ранее было найдено поставившее предыдущий рекорд число M82589933. Новое открытие знаменательно тем, что его совершили, использовав графические процессоры в центрах обработки данных. Первым ресурсы графических процессоров задействовал в 2017 году Михай Преда (Mihai Preda) — он «написал программу GpuOwl для проверки чисел Мерсенна на простоту и сделал своё ПО доступным для всех пользователей GIMPS». В 2023 году к GIMPS подключился Люк Дюран, и участники проекта построили инфраструктуру, необходимую для развёртывания программы Преды на нескольких GPU-серверах в облаке. Работа заняла год, но усилия принесли плоды 11 октября, когда ускоритель Nvidia A100 в ирландском Дублине выдал результат M136279841, а подтвердил его расположенный в техасском Сан-Антонио Nvidia H100. Это интересное упражнение для любителей математики и напоминание, что графические процессоры в ЦОД полезны не только в области искусственного интеллекта. Они могут применяться для моделирования, при котором требуется большое количество исходных данных, для криптографии и многого другого. Мощность графических процессоров растёт, и они продолжат помогать в поиске ещё бо́льших простых чисел. ИИ-модели Google DeepMind решили задачи математической олимпиады на уровне серебряного медалиста
26.07.2024 [10:03],
Владимир Мироненко
Google DeepMind, базирующееся в Лондоне дочернее предприятие Google, специализирующееся на исследованиях в сфере искусственного интеллекта (ИИ), представило ИИ-модели AlphaProof и AlphaGeometry 2, способные решать сложные математические задачи, с которыми не справляются нынешние ИИ-модели. 
Источник изображения: geralt/Pixabay По ряду причин решение математических задач, требующих способности к продвинутым рассуждениям, пока не по силам большинству ИИ-систем. Дело в том, что такие типы задач требуют формирования и использования абстракций. Также требуется сложное иерархическое планирование, постановка подцелей, откат и поиски новых путей, что является сложным вопросом для ИИ. Обе новые ИИ-модели обладают способностью к продвинутым математическим рассуждениям для решения сложных математических задач. AlphaProof была создана с использованием обучения с подкреплением, получив способность доказывать математические утверждения на формальном языке программирования Lean. Для её создания использовалась предварительно обученная языковая модель AlphaZero, алгоритм обучения с подкреплением, который ранее сам себя научил играть в шахматы, сёги и го. В свою очередь, AlphaGeometry 2 представляет собой усовершенствованную версию существующей ИИ-системы AlphaGeometry, представленной в январе и предназначенной для решения задач по геометрии. В то время как AlphaProof была обучена решению задач по широкому кругу математических тем, AlphaGeometry 2 оптимизирована для решения задач, связанных с перемещениями объектов и уравнениями, включающими углы, соотношения и расстояния. Поскольку AlphaGeometry 2 была обучена на значительно большем количестве синтетических данных, чем предшественник, она может справиться с гораздо более сложными геометрическими задачами. Чтобы проверить возможности новых ИИ-систем, исследователи Google DeepMind поручили им решить шесть задач Международной математической олимпиады (IMO) этого года и доказать правильность ответов. AlphaProof решила две задачи по алгебре и одну задачу по теории чисел, одна из которых была самой сложной на олимпиаде, в то время как AlphaGeometry 2 решила задачу по геометрии. Две задачи по комбинаторике остались нерешёнными. Два известных математика, Тим Гауэрс (Tim Gowers) и Джозеф Майерс (Joseph Myers), проверили представленные системами решения. Они присудили каждому из четырёх правильных ответов максимальное количество баллов (семь из семи), что дало системам в общей сложности 28 баллов из максимальных 42. Участник олимпиады, набравший столько же баллов, был бы награждён серебряной медалью и немного не дотянул бы до золота, которое присуждается набравшим 29 баллов и больше. Впервые ИИ-система смогла достичь результатов в решении математических задач IMO на уровне медалиста. «Как математик, я нахожу это очень впечатляющим и значительным скачком по сравнению с тем, что было возможно ранее», — заявил Гауэрс во время пресс-конференции. Создание систем ИИ, способных решать сложные математические задачи, может проложить путь для захватывающего сотрудничества человека и ИИ, считает Кэти Коллинз (Katie Collins), исследователь из Кембриджского университета. Это, в свою очередь, может помочь нам узнать больше о том, как мы, люди, справляемся с математикой. «Мы всё ещё многого не знаем о том, как люди решают сложные математические задачи», — говорит она. |
|
✶ Входит в реестр лиц, организаций и объединений, выполняющих функции иностранного агента; |
© 1997—2026 Электронное периодическое издание "3ДНьюс" | Свидетельство о регистрации СМИ Эл ФС 77-22224
выдано Федеральной Службой по надзору за соблюдением законодательства в сфере массовых коммуникаций и охране культурного наследия
При цитировании документа ссылка на сайт с указанием автора обязательна. Полное заимствование документа является
нарушением
российского и международного законодательства и возможно только с согласия редакции 3DNews.
MWC 2018
2018
Computex
IFA 2018
