Искусственный интеллект: линейная регрессия и методы её обучения / Offсянка

Кто повторяет старое и узнаёт новое, тот может быть предводителем.

Конфуций

В этой статье мы расскажем о линейной регрессии — основополагающем алгоритме, с изучения которого начинается любой курс машинного обучения и науки о данных. Нелегко писать о столь популярном методе, не переходя сразу же на язык формул. К тому же, как ни странно, большее количество доступной информации не всегда способствует лучшему пониманию. Эффективнее всего, конечно, осваивать теорию на реальных проектах, а здесь мы постараемся как можно подробнее рассказать о том, что же такое линейная регрессия и в чём её исключительная ценность. Материал построен таким образом, чтобы вы сами решили, насколько глубоко хотите погрузиться в тему. Однако этой статьи не будет достаточно, чтобы вы смогли реализовать алгоритм с нуля, её главная цель – ваше интуитивное понимание и, конечно, ваш интерес к проблематике ИИ.

⇡#Линейная регрессия: кавер-версия бессмертного хита

Прежде всего необходимо понимать, что линейная регрессия была разработана еще в XIX веке в области статистики для понимания взаимосвязи между данными ввода и вывода. Объяснимость – это одна из главных ценностей, можно сказать, Священный Грааль машинного обучения, к которому так стремятся исследователи ИИ (тот самый explainable AI). Именно объяснимость позволяет сделать наиболее точный прогноз, чем в первую очередь и занимается область прогнозного моделирования (predictive modeling), этой цели и служит вездесущая минимизация ошибки модели. Где только не применяется прогнозное моделирование данных: в сфере бизнеса и финансов, конечно, маркетинге и продажах, удержании клиентов, алгоритмической торговле; в науке – практически во всех сферах. Лишь бы было достаточное количество численных данных, а в них сейчас недостатка нет. Поэтому линейная регрессия была заимствована из статистики и получила такое широкое распространение в сферах машинного обучения и прогнозного моделирования: быстро, понятно, эффективно, открывает простор для творчества.

Кстати, знаете ли вы разницу между машинным обучением и прогнозным моделированием? Напишите, пожалуйста, в комментариях! Ответ будет в следующей статье цикла. А сейчас предлагаем вам погрузиться глубже в тему линейной регрессии (ассоциации с дайвингом настойчиво преследуют автора этой статьи по неизвестной причине).

⇡#Подготовка к погружению: проверка снаряжения

Прежде всего давайте убедимся, что вы знакомы с понятиями, без которых дальше не обойтись.

В контексте машинного обучения линейная регрессия относится к разделу обучения с учителем (supervised learning), то есть когда явно прослеживается связь между вводом и выводом и предсказывается некое значение по ограниченному количеству примеров (на которых, как ученик, обучается алгоритм). Напомним, что обучение с учителем, или контролируемое обучение, делится на две категории: регрессия и классификация (о ней в следующих материалах).

Для обучения с учителем данные мы делим на обучающий (training set) и тестовый наборы (testing set): 80/20 – обычное соотношение. Обучающий набор — это данные, на которых алгоритмбудет учиться. Например, при использовании линейной регрессии точки в обучающем наборе используются для построения линии наилучшего соответствия (line of best fit). Тестовый набор будет использован для оценки качества модели.

На основе обучающих данных мы можем построить график (например, количество часов занятий студента на нем будет обозначено x, а его итоговый балл y) и определить функцию, которая будет очень похожа на этот график. Такую функцию называют функцией гипотезы (hypothesis function), в нашем случае это будет одномерная линейная регрессия (с одной переменной). Теперь на основе функции гипотезы можно сделать прогноз.

Точность функции гипотезы может быть измерена с помощью функции стоимости, или функции потерь. Почему она так называется? Потому что она характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Функция потерь принимает разницу между функцией гипотезы при значениях x и обучающей выборкой при тех же значениях x. Мы стремимся найти параметры функции потерь таким образом, чтобы ее выходные данные были минимальны.

Обучение модели – это и есть минимизация функции потерь, а для этого нужно двигаться в отрицательном направлении производной. Так мы сможем найти такую функцию гипотезы, которая точнее описывает наши обучающие данные. Предположим, что это будет одномерная (простая) линейная регрессия.

⇡#Что это?

Линейная регрессия – это модель линейной зависимости одной (зависимой) переменной от другой или нескольких.

Математическое представление линейной регрессии достаточно легко для восприятия. Линия простой линейной регрессии задается уравнением вида y = β₀ + β₁x, где x – независимая переменная, y – зависимая. Как мы учили в 7 классе!

Простая линейная регрессия с одной независимой переменной (x): красные точки — это реальные значения, линия регрессии (y) — линия наилучшего соответствия, проходящая через точки графика разброса

Наклон линии на этом графике равен коэффициенту β₁, точка пересечения (перехват, intercept) определена в коэффициенте β₀(то есть чему равен y при x = 0)_,этот коэффициент даёт нашей линии свободу передвижения вверх и вниз по двумерному пространству. Алгоритм при обучении стремится найти эти коэффициенты и таким образом определить регрессионную функцию (модель).

Когда на вводе одна переменная (x), это простая линейная регрессия, если их несколько – это уже множественная линейная регрессия. График линейной регрессии в двух измерениях (с единственной независимой переменной) — прямая линия, в трёх — плоскость, в четырёх и более — гиперплоскость.

За этой внешней простотой – огромный потенциал: мы увидим, как на основе этого метода с более чем двухсотлетней историей появилось множество невероятных идей и возможностей. Именно линейная регрессия лежит в основе многих новейших алгоритмов, находящихся на самом острие науки, включая глубокие нейронные сети.

⇡#Как это работает?

Как уже упоминалось, цель алгоритма линейной регрессии – установить такие коэффициенты, чтобы стало возможно определить данную регрессионную модель, а достигается это в процессе обучения. Для этого существует целый ряд методов, однако наиболее популярные из них — это метод обыкновенных наименьших квадратов и краеугольный камень машинного обучения – градиентный спуск.

⇡#Линейная регрессия методом обыкновенных наименьших квадратов: начинаем погружение

Для простоты приведём пример с одной независимой переменной. Предположим, что у нас есть некий набор точек наблюдения. Это может быть площадь квартир, рост людей и т. д., то есть любой фактор (регрессор), влияние которого вы хотите узнать (например, посмотреть зависимость роста и веса, площади жилья и его стоимости и т. д.). Конечно, в реальности чаще принимается во внимание не один фактор, а несколько, но на этот случай у нас есть множественная линейная регрессия.

Данные есть, а теперь вопрос: как прочертить прямую линию, которая была бы максимально приближена к этим точкам наблюдения?

Метод обыкновенных наименьших квадратов (Ordinary Least Squares) предназначен для проведения линии через разброс точек так, чтобы сумма квадратов отклонений точек от линии была минимальной. Простыми словами: ошибка (остаточное значение, отклонение) в данном методе — не что иное, как разница между «реальностью и ожиданием», полученным значением y и прогнозируемым значением ŷ.

e = y — ŷ (Реальное значение — Прогнозированное значение).

Геометрически это сумма длин отрезков между красными крестиками на графике (реальными значениями) и линией регрессии, которую еще называют линией тренда.

Значения ŷ лежат на линии регрессии, а красные крестики обозначают y. e = y — ŷ (Реальное значение — Прогнозированное значение)

Сумма отклонений возводится в квадрат (SSE — sum of squared errors) и минимизируется с помощью дифференциальных и матричных вычислений, которые мы, пожалуй, приводить не будем. Иногда минимизируется не сумма квадратичных отклонений, а среднеквадратичное значение отклонений (MSE — mean of squared errors).

Почему именно квадрат? Я всегда считала, что это делается для избавления от отрицательных значений, однако оказывается, что квадрат длин даёт гладкую функцию (которая имеет непрерывную производную), в то время как просто длина даёт функцию в виде конуса, недифференцируемую в точке минимума. (На тот случай, если любознательность тоже заводит вас далеко).

Метод наименьших квадратов, помимо очевидных достоинств, имеет и существенный недостаток – он плохо справляется с большим количеством данных на вводе (факторов, или попросту x_i). Если вы работаете с большими данными, ваш выбор – это градиентный спуск. Используя этот метод, вы занимаетесь машинным обучением в его классическом виде, потому что именно так обучаются нейросети, включая и сверхсовременные алгоритмы глубокого обучения, которые сейчас на самом острие науки.

⇡#Линейная регрессия методом градиентного спуска

⇡#Градиентный спуск, погружение: уровень 1

Представьте себе, что вы стоите на вершине оврага и хотите спуститься вниз, но не знаете как. Вы будете шагать шире, когда склон более пологий, и мельче, когда склон более крутой. Ваш следующий шаг будет зависеть от предыдущего, а достигнув дна оврага, вы остановитесь. Этот образ поможет вам понять дальнейшие объяснения. Крутизну, или уклон, вашего оврага (крутизну в её первоначальном смысле, конечно!) и будет задавать градиент. Градиент, или уклон (slope), — это не что иное, как отношение изменений по оси y к изменениям по оси x.

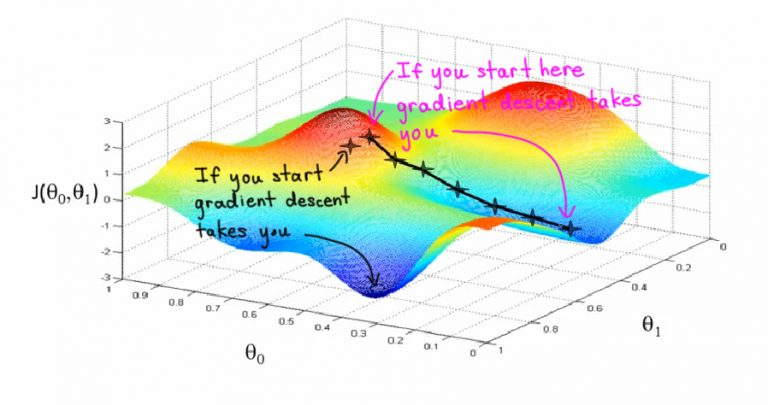
Градиентный спуск – это основной метод обучения нейронных сетей, с его помощью постепенно уточняются параметры нейронной сети (веса и смещение), чтобы таким образом минимизировать функцию потерь сети (cost function, loss function)

⇡#

Цель обучения алгоритма машинного обучения – минимизировать функцию потерь

(Напоминаем, функция потери — разница между значениями меток обучения и прогноза, сделанного с помощью модели). Как это происходит?

Если говорить о простой линейной регрессии ( y = β₀ + β₁ x) в терминах машинного обучения, смещение (intercept) соответствует параметру β₀, а вес (weight) – параметру β₁. Сначала инициируются случайные значения для каждого коэффициента. Сумма квадратов ошибок вычисляется для каждой пары входных и выходных значений. Градиент ошибки будет подсчитываться с использованием частных производных функции потерь по весам и смещению.

Нам понадобится ещё коэффициент скорости обучения (learning rate), он также задается эмпирически. Этот параметр (обычно обозначается £), определяет размер шага по градиенту, выполняемого на каждой итерации, и отвечает за то, как будут корректироваться веса с учётом функции потерь. Чем меньше значение скорости обучения, тем медленнее движение по градиенту. При малом коэффициенте скорости обучения мы, скорее всего, не пропустим ни одной впадины (локального минимума), хотя рискуем застрять на плато, и тогда сходимости придётся подождать.

Процесс повторяется до тех пор, пока не будет достигнута минимальная сумма квадратов ошибок или пока не станет невозможным дальнейшее улучшение.

⇡#Градиентный спуск, погружение: уровень 2

Градиентный спуск — это итеративный метод нахождения локального минимума функции с помощью движения вдоль градиента.

Давайте используем градиентный спуск для обучения простой линейной регрессии. Функцией гипотезы тогда будет линейная функция

Необходимо определить параметры нашей функции гипотезы с помощью функции стоимости, заданной таким образом:

Мы делим на m наши примеры из обучающего набора, обратите внимание, что двойка в знаменателе — это математическая уловка, которую мы используем, чтобы потом компенсировать 2 при взятии производной функции. В скобках разность реальных значений и прогнозов, потом вся она суммируется и возводится в квадрат.

Теперь нужно минимизировать функцию относительно её параметров:

Для простой линейной регрессии эти параметры можно установить равными нулю, а в случае множественной надо будет задать им случайные величины. Подбор параметров осуществляется путем итерации по нашему обучающему набору. Мы будем обновлять параметры согласно такой формуле:

где α – скорость обучения, а – производная, или уклон, функции стоимости, что даёт нам при подстановке

С каждой итерацией параметры будут обновляться, а функция будет стремиться к минимуму.

Вышеописанный алгоритм в англоязычных источниках называется Batch Gradient Descent, поскольку на каждой итерации задействуется весь обучающий набор (batch). Однако существуют такие разновидности этого алгоритма, как стохастический градиентный спуск и мини-пакетный градиентный спуск. Возможно, у вас возникнет желание ознакомиться с ними.

Этот материал создавался с большой надеждой, что машинное обучение постепенно будет восприниматься не как абстрактное и, что уж там, «раскрученное» понятие, а как интереснейшая научная дисциплина.

Другие материалы цикла:

Источники: