Технология T&L (Трансформация и Освещение)

Автор: Кирилл Вишняков

Необходимое вступление

NVIDIA взбудоражила рынок PC выпуском своего GeForce 256™ GPU (Graphics Processing Unit – Графический Процессор). Появление GPU с интегрированными аппаратно геометрическими процессорами и процессорами освещения – прорыв в области 3D-графики, делающий возможным создание приложений качественно нового уровня.

GPU делает доступной графику такого высочайшего уровня, какой еще вчера был возможен только на супер-ЭВМ стоимостью в миллионы долларов. Анимированные персонажи, обрабатываемые GPU, стали настолько детализированными, что видна мимика их лиц, а движения стали плавными. Мир, который населяют эти самые персонажи, теперь естественно отображает органическую жизнь (деревья, кусты, газоны), архитектурные и структурные элементы, которые мы считаем само собой разумеющимися в реальном мире. В до-GPU эпохе стены зданий и помещений изображались с наименьшим возможным количеством деталей, что приводило к 3D-вакууму. Этот вакуум теперь заполнен с помощью GPU элементами реального мира: реалистичная мебель, приборы, источники света, предметы быта и транспортные средства. Короче говоря, мир, формируемый GPU, приблизился к тому, что мы видим в реальности.

• Мощь CPU, расходуемая на обсчет до-GPU мира, сейчас высвободилась для решения других задач: физики, инверсной кинематики, изощренного искусственного интеллекта и т.п. Комбинация GPU и высокопроизводительного CPU предоставляет новые возможности пользователям.
• Этот документ описывает возможности GPU по трансформации и освещению, и каким образом это облегчит жизнь простым пользователям.

Трансформация и освещение

Transform and lighting (T&L) (Трансформация и Освещение) – первые две из четырех ступеней, вычисляемых GPU в 3D-конвейере. Они характеризуются высокой интенсивностью и сложностью вычислений набора очень специфичных математических инструкций (выполняемых миллиарды раз в секунду) для того, чтобы обсчитать сцену.

Для понимания роли T&L, полезно иметь представление о полном процессе создания трехмерной графики, начинающегося непосредственно с приложения. Основные функциональные шаги изображены на Рис. 1.

Рис.1 Графический 3D Конвейер

	Прикладные задачи	Приложение управляет перемещениями объектов (включая камеру) и их взаимодействиями в 3D мире. Проблемы с вычислениями реалистичной физики (объекты обладают моментом) и определениями столкновений/пересечений (мой гоночный автомобиль столкнулся со стеной или другим авто?) отображаются как перемещения объектов в сцене.
	Задачи Уровня Сцены (отсечение, LOD, дисплейный список)	Задачи Уровня Сцены включают в себя отсечение объектов уровня (авто №3 находится полностью позади камеры, так что нет необходимости пересылать его на следующий шаг), выбор соответствующего уровня детализации (авто №1 находится далеко, так что лучше применить низко детализированную модель) и создание списка всех объектов, попадающих в текущее поле зрения камеры.
	Геометрическое преобразование	Геометрический процессор конвертирует 3D данные из одной системы отсчета в другую. Система должна преобразовать данные к текущему виду перед выполнением следующего шага (освещение, триангуляция/разбивка на треугольники и рендеринг). Каждый отображаемый объект и некоторые из неотображаемых должны быть преобразованы каждый раз, когда сцена перерисовывается.
	Освещение	Освещение – следующий шаг в 3D конвейере, производящий к тому же значительное визуальное впечатление. Эффекты освещения служат для повышения реализма сцены и приближению отрендеренных образов еще на один шаг к нашему восприятию реального мира.
	Triangle Setup and Clipping – Разбиение на треугольники и Отсечение	Триангуляционный процессор (процессор треугольников) – математический процессор с плавающей точкой, получающий на входе данные о вершине и выдающий на выходе все необходимые процессору рендеринга обработанные данные. Этот модуль разбивает (sets up) и отсекает (clips) треугольник для передачи его процессору рендеринга.
	Рендеринг	Рендеринг – это расчет правильного цвета для каждого пикселя на экране с учетом всей информации, предоставляемой процессором треугольников. Процессор рендеринга должен учитывать цвет объекта, цвет и направление света, падающего на объект, является ли объект прозрачным и в какой степени, и что за текстуры применены к объекту. Если Рендеринг завершается в несколько этапов, то такой Рендеринг называется многопроходным.

Роль процессора геометрических преобразований (геометрического процессора)

Процессы описания и отображения трехмерных графических объектов и сред весьма сложны. Эта сложность обусловлена тем, что нужно описать 3D-данные последовательно в различных системах координат или в различных системах координат в отдельные, выборочные, моменты времени. Эти различные системы координат описываются как разные "пространства"-“spaces”: мировое пространство (world space), пространство наблюдателя (eye space) и пространство экрана (screen space). Каждое из этих пространств удобно для одной или более операций, необходимых при создании 3D образа. "Мировое пространство" (world space) используется для охвата всех 3D объектов, являющихся частями 3D мира. "Пространство наблюдателя" (eye space) используется для освещения и отсечения, а "экранное пространство" (screen space) используется для сохранения сцены в графическом буфере кадра. Однако, из-за того, что эти пространства используют различные системы координат, 3D данные должны быть конвертированы или "трансформированы" из одного координатного пространства в другое при их перемещении по 3D конвейеру. Геометрический процессор выполняет все эти преобразования аппаратно. На рисунках 2 и 3 изображены примеры мирового пространства и экранного.

Рис.2 Мировое Пространство

Рис.3 Экранное Пространство

Роль Процессора Освещения

Процессор освещения подобен геометрическому процессору, потому что содержит похожий набор математических инструкций, которые и участвуют в вычислении графических функций. GeForce GPU использует раздельные геометрический процессор и процессор освещения для того, чтобы каждый из них мог работать с максимальной эффективностью и не мешая друг другу. Без раздельных процессоров скорость геометрических преобразований ограничена из-за разделения процессорного времени с расчетами освещения. Этот отдельный процессор рассчитывает векторы расстояний от источников света до объектов в 3D сцене и векторы расстояний от объектов до камеры. Вектор, по определению, содержит информацию о направлении и расстоянии. Процессор освещения также отделяет информацию о длине или расстоянии от информации о направлении, потому что это упрощает следующие ступени 3D конвейера. Расчеты освещения используются для освещения вершины, но они также критичны и для других эффектов: различных эффектов тумана, основанных в большей степени на расстоянии от камеры до объекта, а не только на Z-величине объекта.

Почему пользователям нужен интегрированный в GPU геометрический процессор

Раздельные геометрический процессор и процессор освещения, интегрированные в одном чипе, наподобие GeForce GPU, являются абсолютно необходимым условием для наращивания производительности и дополнительных возможностей графических процессоров. В плане попиксельного заполнения и наложения текстур 3D производительность за последние четыре года выросла во много раз. Эти высокие характеристики (fill rate и texture-mapping) предоставили пользователям высокую частоту кадров и плавную навигацию в 3D средах, но оставили задачи расчета геометрических преобразований и освещения на ЦПУ. Это – проблема, т.к. производительность ЦПУ всего лишь удваивается каждые 18 месяцев, в то время как графические процессоры увеличивают свою производительность в восемь раз за тот же промежуток времени.

Расчеты геометрии (T&L) теперь стали главным препятствием на пути к совершенной 3D графике на типичных персональных компьютерах. Графический процессор стал простаивать неоправданно долго в ожидании подготовленных геометрических данных от ЦП. Это узкое место графических процессоров заставляло разработчиков снижать геометрическую детализацию 3D персонажей и сред, ухудшая их визуальное качество для того, чтобы оставить производительность приложения в целом на приемлемом уровне. Интегрированные геометрические процессоры – наиболее оправданный, по соотношению цена/производительность, способ увеличения производительности при расчетах геометрии и предоставляет новые возможности разработчикам приложений для повышения уровня детализации их 3D миров.

Скорость расчета геометрии диктует разработчикам условия того, насколько глубоко они могут тесселировать создаваемые 3D объекты, сколько объектов можно включать в сцену и вообще - насколько детализированным может быть создаваемый ими 3D мир. Тесселяция – это процесс конвертирования (преобразования) кривых линий в последовательность (или ряд) линейных сегментов, наиболее точно аппроксимирующих исходную кривую. Эта идея относится к трехмерным объектам с кривыми поверхностями, преобразуемым в полигоны, аппроксимирующие эти поверхности. Это порождает классическую проблему "производительность-против-качества" для разработчика, потому что более углубленная тесселяция приводит к большому количеству полигонов и, соответственно, к падению производительности, но позволяющая, в итоге, получить высокое качество изображения. На рисунке 4 показан простой пример сферы с различными уровнями тесселяции.

Рис.4 Тесселяция Сферы

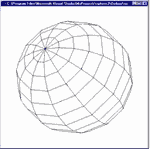
На всех фрагментах Рисунка 4 изображена одна и та же сфера, но на крайнем справа – наиболее детализированная из всех трех. Она содержит в пять раз больше полигонов по сравнению с крайней левой картинкой и в три раза больше по сравнению со средней. Это значит, что правая сфера требует в пять раз более высокой скорости геометрических преобразований по сравнению с левой сферой для того, чтобы общая производительность осталась на прежнем уровне (т.е. не снизилась). Для большинства пользователей персональных компьютеров комфортная частота кадров – от 30 до 60 Гц, поэтому они (пользователи) будут стараться подстроить "качество изображения" (параметры рендеринга, разрешение и т.п.) в настройках программы, чтобы величина fps находилась в указанных пределах.

Эта простая проблема "производительность-против-качества" становится весомой, когда начинаешь понимать, что 3D сцена включает в себя от сотен до тысяч объектов, для каждого из которых надо обсчитать геометрические преобразования и освещение с помощью только лишь ЦП. Программисты должны точно оценить уровень детализации каждой модели в сцене, чтобы точно знать, что соотношение качество/производительность осталось в допустимых пределах. Если сцена представляет собой джунгли, то необходимо включить в неё заросли кустов и деревьев, т.к. одно дерево или кустик не передадут атмосферу джунглей.

Баланс между производительностью и высоким уровнем геометрической детализации (для повышения качества изображения) не был бы таким плохим, если бы не удручающе низкая производительность в геометрических преобразованиях современных ЦПУ. Целью разработки GPU было желание переместить уровень производительности при расчетах с высокой степенью геометрической детализации за тот предел, с которого пользователь начинает ощущать комфорт при работе со сценой. Сегодня действительность такова, что даже топовые модели ЦП заставляют программиста балансировать между производительностью и детализацией, чтобы вожделенный fps попал в диапазон 30 - 60 кадров/сек.

Почему пользователям необходимы интегрированные в GPU процессоры расчета освещения

Интегрированный в GPU расчет освещения – наиболее критичное требование в современной 3D графике, т.к. имеет самое непосредственное отношение к качеству изображения. Расчет освещения – эффективный путь добавления плавных и любых других изменений яркости к 3D объектам, приближающим их по внешнему виду к тому, что мы привыкли видеть в реальности. Возможность реалистичного рендеринга сцены очень важна, т.к. делает восприятие 3D графики доступной и приятной для глаз самой широкой аудитории. Чем выше реалистичность графики 3D сцены, тем больше практических применений она будет иметь. Трехмерные приложения применяются по всюду: от развлечений до образования и науки, промышленности, медицины (синтез лекарств), анализа данных и т.д. Эффекты освещения добавляют выразительности всем 3D приложениям потому, что они придают реалистичную детализированность сцене. Человеческий глаз по своей природе более чувствителен к изменениям яркости (количеству градаций яркости), чем к количеству цветов. Проще говоря, эффекты освещения помогают лучше реализоваться возможностям человеческого глаза. Это означает, что образ со световыми эффектами предоставит наблюдателю гораздо больше информации за определенный промежуток времени, чем без эффектов. На Рисунке 5 изображена архитектурная сцена, демонстрирующая потенциал эффектов освещенности, примененных для добавления реализма сцене.

Рис.5 Пример Освещенности

Без интегрированного расчета освещенности будет невозможно в реальном времени точно отображать изменения свойств освещения 3D объектов при изменении положения камеры относительно источников света – для этого необходимо рассчитывать два важных для точного моделирования физики освещения параметра. Эти два компонента – рассеянный свет и отраженный свет. Под источником рассеянного света понимается источник, излучающий свет во все стороны с одинаковой интенсивностью так, что яркость отраженного от предмета света вообще не зависит от положения камеры. Солнечный свет на игровой площадке – пример рассеянного освещения в реальной жизни. Яркость объекта в 3D сцене прежде всего определяется расчетами рассеянного освещения. Отраженный свет отличен от рассеяного, т.к. зависит от положения камеры, направления на источник света и ориентации треугольника перед рендерингом. Сверкающий блик света на экране телевизора в темном углу комнаты поможет вам яснее представить отраженное освещение. Отраженный свет зависит от отражающей способности объектов, дающей эффект отражения и блика. На Рисунке 6 показаны два примера космической станции из теста 3DWinBench с эффектами рассеянного и отраженного света.

Блики отраженного света перемещаются по объекту, если движется камера, или же сам объект относительно источника света. По этой причине они не могут быть заранее посчитаны и заданы в статике. Отраженное освещение особенно полезно для двух эффектов в 3D сцене: для отображения изменений при смене положения и имитации объектов из материалов с разными свойствами.

Отраженный свет также важен при присвоении свойств различных материалов объектам в 3D сцене. Шёлковая рубашка выглядит иначе, чем хлопковая, даже если они одного цвета. Возможное отличие заключается в том, как эти два материала отражают свет или, иными словами, излучают отражённый свет. Другой пример – полированный костяной шарик в сравнении с шариком из того же материала, но до полировки. Полирование не меняет цвет или структуру шарика, оно изменяет характеристику направленности отраженного света. Отраженный свет в комбинации с наложением соответствующей текстуры придает объекту более реалистичный вид - он приобретает свойства объекта из реального мира, т.е. они становятся внешне похожими.

Отраженный свет может быть получен и без специализированного аппаратного процессора освещения, но при это производительность резко упадет. Наложение текстуры может быть использовано для некоторых отражающих световых эффектов, но если камера движется вокруг сцены, то карты среды должны все время пересчитываться, если аппаратная поддержка есть только наложения кубических карт отображения среды. Сферические карты отображения – общепринятая альтернатива, но этот способ чреват проблемами с производительностью и качеством изображения, делая невозможным получение интерактивной 3D среды.

Где работают Transform & Lighting (T&L) - Трансформация и Освещение:
Миграция с CPU на GPU

Вся работа в графическом 3D конвейере поделена между центральным процессором и графическим процессором. Грань, определяющая уровень разделения задач центрального процессора и графического процессора в конвейере, постоянно поднимается. 1999 год – год, когда графические процессоры с интегрированными T&L процессорами стали доступны по цене большинству пользователей персональных компьютеров. Рисунок 8 демонстрирует все возрастающую роль специализированных графических процессоров в основной массе персональных компьютеров за последние несколько лет. Сегодня графический процессор полностью обсчитывает все стадии графического конвейера, что и подразумевает термин GPU.

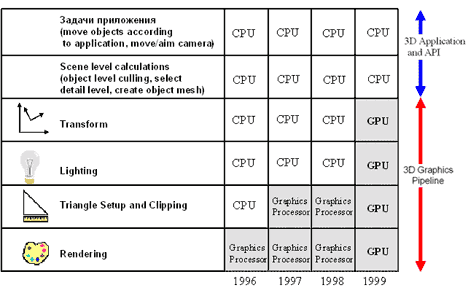
Функции трансформации и освещения в графическом 3D конвейере традиционно решались с помощью возможностей доступных на рынке универсальных процессоров – для PC это значило использование центрального процессора. Это было вызвано тем, что для решения этих задач (T&L) требовались возможности процессора с плавающей точкой, а математический процессор уже в то время являлся обязательной составной частью универсальных процессоров (FPU). Стоимость реализации была естественным препятствием на пути добавления возможностей T&L в графические программы на персональных компьютерах.

Понятие стоимости было неактуально для экзотических Unix-станций, где цена неинтегрированных (дискретных) геометрических процессоров и процессоров освещения не имела значения из-за неограниченного бюджета. Как только за последующие 2 года затраты снизились, рабочие станции на Windows NT предоставили для бизнеса эти новые возможности, но с помощью составных графических плат расширения, стоящих тысячи долларов. Цены продолжали падать по мере того, как производители полупроводников умудрялись втискивать на один кристалл все больше и больше транзисторов. В 1999 году стало возможным отказаться от GPU с отдельными процессорами геометрии и освещения, т.к. теперь появилась возможность интегрировать эти процессоры на одном кристалле с другими компонентами графического 3D конвейера. Новейшие кремниевые технологии разрушили этот ценовой барьер и позволили nVidia интегрировать все компоненты конвейера в одном кристалле GPU и предложить его на рынке по приемлемой цене.

Сейчас, когда GPU стал доступен в PC верхней ценовой категории, системные дизайнеры выбирают этот новый путь, чтобы сделать доступными ошеломляющие визуальные возможности широкому кругу пользователей. Две характерных черты архитектуры:

• Более высокая графическая производительность: GPU с интегрированными T&L процессорами обрабатывают эти функции от 2 до 4 раз быстрее топовых моделей ЦПУ;
• Мощь ЦПУ может быть теперь с толком использована для обсчета физики, искусственного интеллекта, других прикладных функций и управления системными ресурсами.

GPU с легкость превосходят по производительности центральные процессоры по той простой причине, что они (GPU) "заточены" исключительно под несколько узкоспециализированных, нацеленных исключительно на графику, математических функций. Математический сопроцессор (FPU) центрального процессора должен обрабатывать множество и других функций широкого применения, т.к. этого требует его универсальная природа. GPU не так универсальны, но зато исключительно производительны в узком наборе графических функций.

Математические требования к GPU четко определены. T&L вычисления целиком и полностью основаны на матричных вычислениях, специфичном перемножении 4x4 матриц и некоторых других векторных операциях. Строго определенное количество инструкций (операций) процессоров T&L весьма полезно для максимальной оптимизации их архитектуры для получения наивысшей кремниевой эффективности. Эта самая кремниевая эффективность делает легко предсказуемой и наивысшую производительность GPU. Это предположение основано на том, что буферы и конвейеры могут быть очень сильно оптимизированы в соответствии с крайне узким набором специфичных требований. Когда вычисления T&L возложены на ЦПУ, то производительность очень сильно колеблется, т.к. процессор вынужден делить эти вычисления с другими задачами общего характера. Большинство современных процессоров имеют специальные математические расширения команд (типа MMX, SSE, SSE2, 3DNow! и т.п.), но эти расширения также являются универсальными. Эти расширения предназначены для обработки функций мультимедиа (аудио, видео) и алгоритмов связи.

Хитовая 3D игра, запускаемая на GPU, должна быть большим, чем просто демонстрашкой прекрасной графики и "усладой для глаз". Она нуждается в изощренном искусственном интеллекте, реалистичной физике и целом комплексе игровых элементов. Потребность в мощном искусственном интеллекте в стратегиях и спортивных играх в до-GPU эпоху наделила персонажи убогим, плохо детализированным внешним видом. Разработчики были вынуждены жертвовать графическими возможностями игры в пользу задач искусственного интеллекта и физики, которые также возлагались на центральный процессор. GPU делает возможным для игроков в командные волейбол, футбол и баскетбол бегать, прыгать и смотреть как реальным игрокам. Моделирование реалистичной физики дополняет возможности 3D приложений, позволяя точно имитировать реальный мир. Объекты реального мира обладают моментом, точно так же должны его иметь и объекты 3D приложения. Эти функции сами по себе могут "заткнуть" современный топовый центральный процессор, ведь ЦПУ все еще выполняет и традиционные функции типа управления трафиком по шинам, запросы служб операционных систем и все запросы приложений. Эти функции не могут быть переложены на графический процессор, но функции GPU будут сняты с центрального процессора, а уже одно это значительно улучшает графическую производительность и производительность приложения в целом.

Пользователь PC – безоговорочный победитель

Пользователи персональных компьютеров – безоговорочные победители, т.к. операции T&L теперь перенесены с ЦПУ на GPU и новая архитектура просто поразительно увеличивает общую производительность при неизменной цене. Высочайшая производительность – результат эффективного разделения задач между различными процессорами в персональном компьютере. Преимущества этого весьма существенны:

• Уже существующие 3D приложения получают прирост производительности;
• Программисты теперь могут использовать больше продвинутых эффектов и графических техник (приемов), так что графика в их приложениях станет более информативной и приятно выглядящей;
• Новые приложения, использующие 3D, постепенно заменят базирующийся на WYSIWYG дву-мерный растровый графический интерфейс так же, как он вытеснил интерфейс текстовой строки.

Эти преимущества тем больше, чем больше графическая производительность PC. GPU, типа GeForce, задают новое соотношение цена/производительность для типичного пользователя PC. Это соотношение стало впервые оптимальным в 1999 году и с тех пор только улучшается, т.к. на рынке появляется все больше различных моделей и графических процессоров с интегрированными процессорами T&L и все возрастающей производительностью и функциональностью.

Приложение A

Как работают Трансформация и Освещение: математика вслед за магией

Операции при выполнении Трансформации и Освещения сходны, т.к. требуют повторения вычислений определенного набора математических функций много миллионов раз в секунду. Специфические математические требования, предъявляемые к GPU, описаны здесь, так что читатель может легко разобраться почему эти функции так сильно подвержены оптимизации и приспособлены для специализированных процессоров больше, чем для универсальных ЦПУ.

Операция трансформации – это операция умножения матрицы 4x4. Вектор, представляющий 3D данные, обычно содержит вершину или вектор нормали, помноженный на матрицу 4x4, называемую матрицей трансформаций и результат – трансформированный вектор. Чтобы это сделать, спецпроцессор трансформаций использует стандартную линейную алгебру для умножения матриц. На Рисунке 9 показан универсальный пример этой операции.

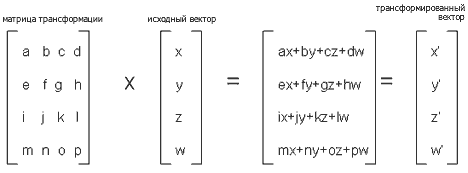
Перед тем, как трансформировать вектор, необходимо построить матрицу трансформаций. Эта матрица содержит всю необходимую информацию для конвертирования данных вектора в новую координатную систему. Промежуточная матрица создается для всех операций (масштабирование, вращение и смещение), которые должны быть выполнены над вектором, а затем все промежуточные матрицы перемножаются, чтобы получить единственную матрицу, которая и будет содержать итоговый результат всех операций. Эта одиночная матрица называется матрицей трансформаций и может многократно использоваться без перерасчета. Например, если матрица трансформаций уже создана, то она может с успехом использоваться для преобразования как одного вектора, так и целого миллиона. Эта способность к многократному использованию матрицы трансформаций весьма эффективно экономит время, необходимое для ее перерасчета.

Сперва может показаться, что достаточно матрицы размерностью 3x3, лишь потому, что это расчеты 3D графики. Четвертый компонент в исходном векторе – w. W используется в качестве коэффициента масштабирования при перспективной коррекции и дополняет матрицу трансформаций до размерности 4x4. Углубленное обсуждение параметра w лежит за границами этого документа.

Заметим, что количество математических операций для одного геометрического преобразования постоянно: 16 операций умножения и 12 операций сложения. Сама математика, требуемая для геометрических преобразований, так же весьма проста – используется только умножение и сложение.

Частью, относящейся к волшебству, при перемножении матриц во время геометрических преобразований является то обстоятельство, что масштабирование, вращение и трансляция – все эти операции могут выполняться параллельно, в один и тот же промежуток времени. Это делает производительность специализированного геометрического процессора величиной легко определяемой и более-менее постоянной. А это, в свою очередь, позволяет программистам реально оценить, на сколько их приложение будет "грузить" геометрию, чтобы сохранить достаточно приемлемый баланс производительность/качество.

Расчеты освещенности весьма требовательны к вычислительной мощности. Типичные расчеты освещенности вычисляют расстояние и направление между источниками света и объектами. Процессоры освещенности производят так же функции преобразования некоторых данных типа создания векторов нормали для треугольников и вершин, а так же "нормализации" этих векторов. Нормализация вектора – это процесс его преобразования в новый вектор с длиной равной единице по модулю и ориентированным так же, как и оригинальный вектор. Вектор "нормали" к вершине или треугольнику по определению – вектор, строго перпендикулярный треугольнику или вершине. Перпендикуляр к вершине определяется как перпендикуляр к поверхности, которую эта вершина описывает.

Здесь описана математика простейшей модели освещения. Вычисление разностных векторов требует только сложения (вычитание – это просто добавление отрицательного значения) данных xyz для каждого из объектов и поэтому требует три операции сложения. Для примера - разностный вектор между источником света #1 с координатами (x1, y1, z1) и объектом #2 с координатами (x2, y2, z2):

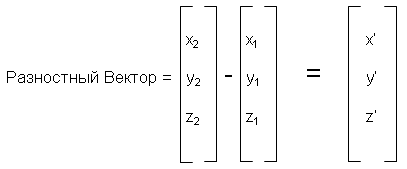
Эти векторы далее должны быть переработаны в скалярную величину расстояния и нормализованный вектор перед тем, как отправиться в процессор освещенности. Эти операции очень ресурсоемки, но совершенно необходимы потому, что представление разностных векторов как отдельных величин для расстояния и направления значительно упрощает последующие шаги в 3D конвейере. Вычисление расстояния – сложение квадратов величин x, y и z с последующим извлечением квадратного корня из этой суммы, как показано в Уравнении 1:

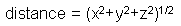
Нормализация вектора требует деления каждого из значений x, y и z на расстояние. Так что процессор освещения должен уметь как прибавлять, так и делить.

В статье использованы материалы с сайтов: www.nvidia.com, www.tomshardware.com и ряда других.

Дополнительные материалы

• Что такое T&L. Часть 1
• Что такое T&L. Часть 2